
| 已知二次函數f(x)=x2-ax+a(x∈R)同時滿足:(1)不等式f(x)≤0 的解集有且只有一個元素;(2)在定義域內存在0<x1<x2,使得不等式f(x1)>f(x2)成立。設數列{an}的前n項和Sn=f(n), (1)求數列{an}的通項公式; (2)設 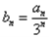 ,求數列{bn}的前n項和; ,求數列{bn}的前n項和;(3)設各項均不為零的數列{cn}中,所有滿足cici+1<0的正整數的個數稱為這個數列{cn}的變號數。另 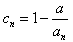 (n為正整數),求數列{cn}的變號數。 (n為正整數),求數列{cn}的變號數。 |
| 解:(1)∵不等式f(x)≤0 的解集有且只有一個元素, ∴ 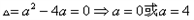 , ,∵在定義域內 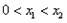 ,使得不等式 ,使得不等式 成立, 成立,∴函數y=f(x)在(0,+∞)上是遞減函數, 當a=0時,函數f(x)=x2在(0,+∞)上遞增, 故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立, 當a=4時,函數f(x)=x2-4x+4在(0,2)上遞減, 故存在0<x1<x2,使得不等式f(x1)>f(x2)成立; 綜上,得 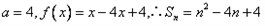 , ,當n=1時, 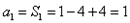 ; ;當n≥2時, 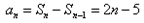 ; ;∴ 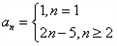 ; ;(2)∵ 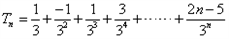 , ① , ①∴ 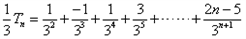 , ② , ②①-②得: 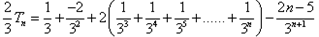 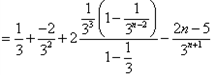 , ,∴ 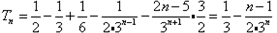 ; ;(3)由題設 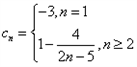 , ,∵n≥3時, 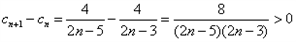 , ,∴n≥3時,數列{cn}遞增, ∵  ,由 ,由 ,可知 ,可知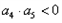 , ,即n≥3時,有且只有1個變號數, 又∵ 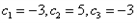 ,即 ,即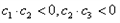 , ,∴此處變號數有2個, 數列{cn}共有3個變號數,即變號數為3。 |


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| f(x) | x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com