
(1)寫出明年第x個月的需求量g(x)(萬件)與月份x的函數關系,并求出哪個月份的需求量最大,最大需求量是多少?
(2)如果將該商品每月都投放市場p萬件(銷售未完的商品都可以在以后各月銷售),要保證每月都足量供應,問p至少為多少萬件?
解:(1)g(1)=f(1)=![]() ×1×2×33=
×1×2×33=![]() (萬件).
(萬件).
當x≥2時,g(x)=f(x)-f(x-1)
=![]() x(x+1)(35-2x)-
x(x+1)(35-2x)-![]() (x-1)x(37-2x)
(x-1)x(37-2x)
=![]() x·[(35+33x-2x2)-(-37+39x-2x2)]=
x·[(35+33x-2x2)-(-37+39x-2x2)]=![]() x·(72-6x)=
x·(72-6x)=![]() x·(12-x)
x·(12-x)
當x=1時,g(x)也成立.
∴g(x)=![]() x(12-x)(x∈N*,且x≤12).
x(12-x)(x∈N*,且x≤12).
∵g(x)≤![]() [
[![]() ]2=
]2=![]() .
.
∴當x=12-x,即x=6時,g(x)max=![]() (萬件),
(萬件),
故6月份該商品的需求量最大,最大需求量為![]() 萬件.
萬件.
(2)依題意,對一切x∈{1,2,…,12}有
px≥g(1)+g(2)+…+g(x)=f(x).
∴p≥![]() (x+1)(35-2x)(x=1,2,…,12).
(x+1)(35-2x)(x=1,2,…,12).
∵h(x)=![]() (35+33x-2x2)
(35+33x-2x2)
=![]() [
[![]() -2(x-
-2(x-![]() )2]
)2]
∴h(x)max=h(8)=1.14.
故p≥1.14,
故每個月至少投入1.14萬件,才可以保證每個月都保證供應.


科目:高中數學 來源: 題型:
| 1 | 150 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 150 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 150 |
查看答案和解析>>
科目:高中數學 來源:2011年高三數學第一輪基礎知識訓練(26)(解析版) 題型:解答題
 x(x+1)(35-2x)(x∈N*,且x≤12).
x(x+1)(35-2x)(x∈N*,且x≤12).查看答案和解析>>
科目:高中數學 來源:2012屆福建省四地六校聯考上學期高三第三次月考理科數學試卷 題型:解答題
某地區預計明年從年初開始的前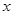 個月內,對某種商品的需求總量
個月內,對某種商品的需求總量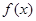 (萬件)與月份
(萬件)與月份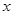 的近似關系為
的近似關系為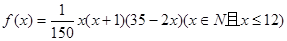 .
.
(1)寫出明年第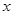 個月的需求量
個月的需求量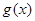 (萬件)與月份
(萬件)與月份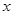 的函數關系式,并求出哪個月份的需求量超過1.4萬件;
的函數關系式,并求出哪個月份的需求量超過1.4萬件;
(2)如果將該商品每月都投放市場p萬件,要保持每月都滿足市場需求,則p至少為多少萬件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com