從正方體的8個頂點中選取4個點,連接成一個四面體,這個四面體可能為:
①每個面都是直角三角形;
②每個面都是等邊三角形;
③有且只有一個面是直角三角形;
④有且只有一個面是等邊三角形.
其中正確的說法有 .(寫出所有正確結論的編號).
【答案】
分析:我們把正方體中的所有三棱錐分為兩類:第一類:在底面ABCD的三個頂點中任取三個作為三棱錐的頂點,然后在底面A
1B
1C
1D
1的四個頂點中任取一個作為三棱錐的第四個頂點,
第二類:在底面ABCD的三個頂點中任取兩個作為三棱錐的頂點,然后在底面A
1B
1C
1D
1的四個頂點中任取兩個作為三棱錐的另外兩個頂點,從而得出正方體中的所有三棱錐的情況.
解答:解:我們把正方體中的所有三棱錐分為兩類:第一類:在底面ABCD的三個頂點中任取三個作為三棱錐的頂點,然后在底面A
1B
1C
1D
1的四個頂點中任取一個作為三棱錐的第四個頂點,一種是如圖(1)中的三棱錐A
1-ABD,其中三個面是直角三角形,
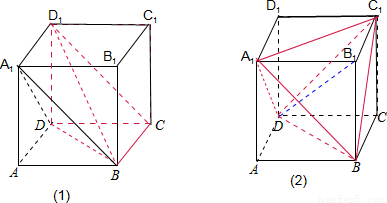
第四個 面是等邊三角形;另一種是如圖(1)中的三棱錐D
1-BCD,四個面都是直角三角形.
第二類:在底面ABCD的三個頂點中任取兩個作為三棱錐的頂點,然后在底面A
1B
1C
1D
1的四個頂點中任取兩個作為三棱錐的另外兩個頂點,一種是如圖(2)中的三棱錐A
1-BC
1D,其中四個面是等邊三角形;另一種是如圖(2)中的三棱錐A
1-BB
1D,其中三個面是直角三角形,第四個面是等邊三角形.
綜上可知:①②④正確,而③不可能有.
故答案為①②④.
點評:對正方體中的所有三棱錐進行正確分類是解題的關鍵.



