
【題目】已知圓![]() :
:![]() 內一點
內一點![]() ,
,![]() 點為圓
點為圓![]() 上任意一點,線段
上任意一點,線段![]() 的垂直平分線與線段
的垂直平分線與線段![]() 連線交于點
連線交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,求
,求![]() 的內切圓半徑的最大值.
的內切圓半徑的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根據線段中垂線的性質可得,|MP|=|MQ|,又|MQ|+|M![]() |=4,故有|M
|=4,故有|M![]() |+|MP|=4>|P
|+|MP|=4>|P![]() |,根據橢圓的定義判斷軌跡橢圓,求出
|,根據橢圓的定義判斷軌跡橢圓,求出![]() 值,即得橢圓的標準方程;
值,即得橢圓的標準方程;
(2)設![]() ,
,![]() ,設
,設![]() 的內切圓的半徑為
的內切圓的半徑為![]() ,當
,當![]() 最大,
最大,![]() 就最大,利用直線和橢圓的位置關系求出
就最大,利用直線和橢圓的位置關系求出![]() 最大值,進而可得
最大值,進而可得![]() 的最大值.
的最大值.
(1)由圓的方程可知,圓心![]() (1,0),半徑等于4,設點M的坐標為
(1,0),半徑等于4,設點M的坐標為![]() ,
,
∵PQ的垂直平分線交![]() Q于M,
Q于M,
∴|MP|=|MQ|.
又|MQ|+|M![]() |=4(半徑),
|=4(半徑),
∴|M![]() |+|MP|=4>|A
|+|MP|=4>|A![]() |=2.
|=2.
∴點M滿足橢圓的定義,且2![]() =4,2
=4,2![]() =
=
∴![]() =2,
=2,![]() =1,
=1,![]() ,
,
∴點M的軌跡方程為![]() ;
;
(2)設![]() ,
,![]() ,設
,設![]() 的內切圓的半徑為
的內切圓的半徑為![]() ,因為
,因為![]() 的周長為
的周長為![]() ,
,![]() ,因此
,因此![]() 最大,
最大,![]() 就最大,
就最大,
![]() ,由題意知,直線
,由題意知,直線![]() 的斜率不為零,可設直線
的斜率不為零,可設直線![]() 的方程為
的方程為![]() ,
,
由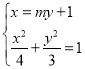 得
得![]() ,
,
所以![]() ,
,![]() ,
,
又因直線![]() 與橢圓
與橢圓![]() 交于不同的兩點,故
交于不同的兩點,故![]() ,即
,即![]() ,
,![]() ,則
,則![]()
![]() ,
,
令![]() ,則
,則![]() ,
,
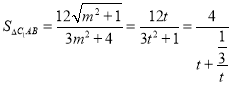 ,令
,令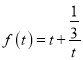 ,
,
由函數的性質可知,函數![]() 在
在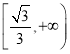 上是單調遞增函數,即當
上是單調遞增函數,即當![]() 時,
時,![]() 在
在![]() 上單調遞增,因此有
上單調遞增,因此有![]() ,所以
,所以![]() ,
,
即當![]() ,
,![]() 時,
時,![]() 最大,此時
最大,此時![]() ,故當直線
,故當直線![]() 的方程為
的方程為![]() 時,
時,![]() 內切圓半徑的最大值為
內切圓半徑的最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知斜三棱柱![]() 中,
中,![]() ,
,![]() 在底面
在底面![]() 上的射影恰為
上的射影恰為![]() 的中點
的中點![]() ,且
,且![]() .
.
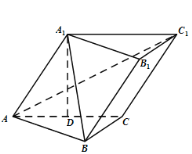
(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的平面角為
的平面角為![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 點在底面
點在底面![]() 內的射影
內的射影![]() 在線段
在線段![]() 上,且
上,且![]() ,
, ![]() ,M在線段
,M在線段![]() 上,且
上,且![]() .
.
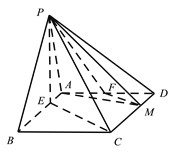
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)在線段AD上確定一點F,使得平面![]() 平面PAB,并求三棱錐
平面PAB,并求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某樂園按時段收費,收費標準為:每玩一次不超過![]() 小時收費10元,超過
小時收費10元,超過![]() 小時的部分每小時收費
小時的部分每小時收費![]() 元(不足
元(不足![]() 小時的部分按
小時的部分按![]() 小時計算).現有甲、乙二人參與但都不超過
小時計算).現有甲、乙二人參與但都不超過![]() 小時,甲、乙二人在每個時段離場是等可能的。為吸引顧客,每個顧客可以參加一次抽獎活動。
小時,甲、乙二人在每個時段離場是等可能的。為吸引顧客,每個顧客可以參加一次抽獎活動。
(1) 用![]() 表示甲乙玩都不超過
表示甲乙玩都不超過![]() 小時的付費情況,求甲、乙二人付費之和為44元的概率;
小時的付費情況,求甲、乙二人付費之和為44元的概率;
(2)抽獎活動的規則是:顧客通過操作按鍵使電腦自動產生兩個[0,1]之間的均勻隨機數![]() ,并按如右所示的程序框圖執行.若電腦顯示“中獎”,則該顧客中獎;若電腦顯示“謝謝”,則不中獎,求顧客中獎的概率.
,并按如右所示的程序框圖執行.若電腦顯示“中獎”,則該顧客中獎;若電腦顯示“謝謝”,則不中獎,求顧客中獎的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】檳榔原產于馬來西亞,中國主要分布在云南、海南及臺灣等熱帶地區,在亞洲熱帶地區廣泛栽培.檳榔是重要的中藥材,在南方一些少數民族還有將果實作為一種咀嚼嗜好品,但其被世界衛生組織國際癌癥研究機構列為致癌物清單Ⅰ類致癌物.云南某民族中學為了解![]() ,
,![]() 兩個少數民族班學生咀嚼檳榔的情況,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周咀嚼檳榔的顆數作為樣本繪制成莖葉圖如圖所示(圖中的莖表示十位數字,葉表示個位數字).
兩個少數民族班學生咀嚼檳榔的情況,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周咀嚼檳榔的顆數作為樣本繪制成莖葉圖如圖所示(圖中的莖表示十位數字,葉表示個位數字).
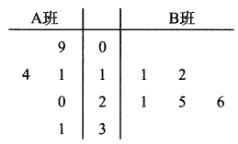
(1)你能否估計哪個班級學生平均每周咀嚼檳榔的顆數較多?
(2)從![]() 班的樣本數據中隨機抽取一個不超過19的數據記為
班的樣本數據中隨機抽取一個不超過19的數據記為![]() ,從
,從![]() 班的樣本數據中隨機抽取一個不超過21的數據記為
班的樣本數據中隨機抽取一個不超過21的數據記為![]() ,求
,求![]() 的概率;
的概率;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四面體A-BCD中,有兩條棱的長為![]()
![]() ,其余棱的長度都為1;
,其余棱的長度都為1;
(1)若![]() ,且
,且![]() ,求二面角A-BC-D的余弦值;
,求二面角A-BC-D的余弦值;
(2)求a的取值范圍,使得這樣的四面體是存在的;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com