
在某服裝批發市場,某種品牌的時裝當季節將來臨時,價格呈上升趨勢,設這種時裝開始時定價為20元,并且每周(7天)漲價2元,從第6周開始保持30元的價格平穩銷售;從第12周開始,當季節即將過去時,平均每周減價2元,直到第16周周末,該服裝不再銷售。
⑴試建立銷售價y與周次x之間的函數關系式;
⑵若這種時裝每件進價Z與周次 次之間的關系為Z=
次之間的關系為Z= ,1≤
,1≤ ≤16,且
≤16,且 為整數,試問該服裝第幾周出售時,每件銷售利潤最大?最大利潤為多少?
為整數,試問該服裝第幾周出售時,每件銷售利潤最大?最大利潤為多少?
⑴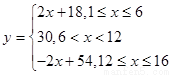 ⑵在第6周時出售每件銷售利潤最,最大
⑵在第6周時出售每件銷售利潤最,最大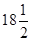 元.
元.
【解析】
試題分析:(1)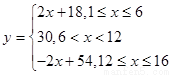
(2)設每件銷售利潤為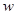 元,
元,
當1≤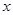 ≤6時,
≤6時,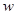 = y-Z=2
= y-Z=2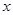 +18+ 0.125(
+18+ 0.125(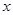 -8)
-8) -12=
-12=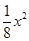 +14
+14
有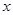 =6時,
=6時,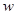 最大值=
最大值=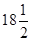 ;
;
當6<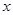 <12時,
<12時,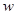 = y-Z="30+" 0.125(
= y-Z="30+" 0.125(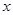 -8)
-8) -12=0.125(
-12=0.125(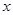 -8)
-8) +18
+18
有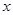 =8時,
=8時,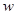 最大值=18
最大值=18
當12≤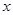 ≤16時
≤16時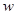 = y-Z=-2
= y-Z=-2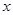 +54+ 0.125(
+54+ 0.125(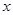 -8)
-8) -12=0.125(
-12=0.125(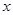 -16)
-16) +18
+18
有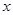 =16時,
=16時,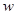 最大值=18
最大值=18
綜上所述:在第6周時出售每件銷售利潤最,最大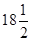 元.
元.
考點:二次函數的應用
點評:本題考查的是二次函數的運用,由于計算量大,考生在做這些題的時候要耐心細心.難
度中上.此題是分段函數,題目所涉及的內容在求解過程中,要注意分段函數問題先分段解
決,最后再整理、歸納得出最終結論,另外還要考慮結果是否滿足各段的要求,這是解此類
綜合應用題目的特點.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| 1 | 8 |
查看答案和解析>>
科目:高中數學 來源:新課標教材全解高中數學人教A版必修1 人教A版 題型:044
在某服裝批發市場,季節性服裝當季節即將來臨時,價格呈上升趨勢,設某服裝開始時定價為10元,并且每周(7天)漲價2元,5周后開始保持20元的價格平穩銷售;10周后當季節即將過去時,平均每周削價2元,直到16周末,該服裝已不再銷售.
(1)試建立價格p(元)與周次t之間的函數關系;
(2)若此服裝每周進價q(元)與周次t之間的關系式為q=-0.125(t-8)2+12,t∈[0,16],t∈N,試問該服裝第幾周每件銷售利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
在中國輕紡城批發市場,季節性服裝當季節即將來臨時,價格呈上升趨勢. 設某服裝開始時定價為 10 元,并且每周(7 天)漲價 2 元,5 周后開始保持 20 元的平穩銷售;10 周后當季節即將過去時,平均每周降價 2 元,直到 16 周末,該服裝已不再銷售.
(1)試建立價格![]() 與周次
與周次![]() 之間的函數關系;
之間的函數關系;
(2)若此服裝每件進價![]() 與周次
與周次![]() 之間的關系式
之間的關系式![]() ,
,
![]() ,問該服裝第幾周每件銷售利潤最大?
,問該服裝第幾周每件銷售利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com