
【題目】已知函數![]() .
.
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)若![]() ,求證:
,求證:![]() .
.
【答案】(Ⅰ)見解析(Ⅱ)見證明
【解析】
(Ⅰ)利用導數與函數單調性的關系求解;
(Ⅱ)af(x)>lnx![]() .令F(x)
.令F(x)![]() ,F′(x)
,F′(x)![]() (x>0).
(x>0).
①當∈(0,1]時,F′(x)<0,F(x)單調遞減,F(x)≥F(1)=ae>0;
②當>1時,令G(x)![]() ,利用導數求得最小值大于0即可.
,利用導數求得最小值大于0即可.
解.(1)f(x)的定義域為(﹣∞,0)∪(0,+∞),
∵![]() ,
,
∴x∈(﹣∞,0),(0,1)時,f′(x)<0,x∈(1,+∞)時,f′(x)>0
∴函數f(x)的單調增區間為:(1,+∞),減區間為(﹣∞,0),(0,1).
(2)af(x)>lnx![]() .
.
令F(x)![]() ,
,
F′(x)![]() .(x>0).
.(x>0).
①當x∈(0,1]時,F′(x)<0,F(x)單調遞減,F(x)≥F(1)=ae>0;
②當x>1時,令G(x)![]() ,G
,G![]() .
.
∴G(x)在(1,+∞)單調遞增,
∵x→1時,G(x)→﹣∞,G(2)=e2![]() 0,
0,
∴G(x)存在唯一零點0∈(1,2),
F(x)min=F(x0)![]()
∵G(x0)=0,![]() .
.
綜上所述,當![]() 時,af(x)>lnx成立.
時,af(x)>lnx成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】為了解男性家長和女性家長對高中學生成人禮儀式的接受程度,某中學團委以問卷形式調查了![]() 位家長,得到如下統計表:
位家長,得到如下統計表:

(1)據此樣本,能否有![]() 的把握認為“接受程度”與家長性別有關?說明理由;
的把握認為“接受程度”與家長性別有關?說明理由;
(2)學校決定從男性家長中按分層抽樣方法選出![]() 人參加今年的高中學生成人禮儀式,并從中選
人參加今年的高中學生成人禮儀式,并從中選![]() 人交流發言,設
人交流發言,設![]() 是發言人中持“贊成”態度的人數,求
是發言人中持“贊成”態度的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
參考數據
|
|
|
|
|
|
參考公式
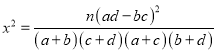
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經銷商銷售某種產品,在一個銷售季度內,每售出![]() 該產品獲利潤
該產品獲利潤![]() 元;未售出的產品,每
元;未售出的產品,每![]() 虧損
虧損![]() 元.根據以往的銷售記錄,得到一個銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了
元.根據以往的銷售記錄,得到一個銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了![]() 該產品.用
該產品.用![]() (單位:
(單位:![]() ,
,![]() )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量,![]() (單位:元)表示下一個銷售季度內經銷該產品的利潤.
(單位:元)表示下一個銷售季度內經銷該產品的利潤.

(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)根據直方圖估計利潤![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域為R,對任意實數x,y滿足f(x+y)=f(x)+f(y)+![]() ,且f(
,且f(![]() )=0,當x>
)=0,當x>![]() 時,f(x)>0.給出以下結論
時,f(x)>0.給出以下結論
①f(0)=-![]()
②f(-1)=-![]()
③f(x)為R上減函數
④f(x)+![]() 為奇函數;
為奇函數;
⑤f(x)+1為偶函數
其中正確結論的有( )個
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log4(4x+1)+kx(k∈R)是偶函數.
(1)求k的值;
(2)若函數y=f(x)的圖象與直線y=![]() x+a沒有交點,求a的取值范圍;
x+a沒有交點,求a的取值范圍;
(3)若函數h(x)=![]() +m2x-1,x∈[0,log23],是否存在實數m使得h(x)最小值為0,若存在,求出m的值;若不存在,請說明理由.
+m2x-1,x∈[0,log23],是否存在實數m使得h(x)最小值為0,若存在,求出m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐PABCD的底面ABCD是矩形,PA⊥底面ABCD,點E、F分別是棱PC、PD的中點,則
①棱AB與PD所在直線垂直;
②平面PBC與平面ABCD垂直;
③△PCD的面積大于△PAB的面積;
④直線AE與直線BF是異面直線.
以上結論正確的是________.(寫出所有正確結論的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓的離心率為![]() ,以該橢圓上的點和橢圓的左、右焦點
,以該橢圓上的點和橢圓的左、右焦點![]() 為頂點的三角形的周長為
為頂點的三角形的周長為![]() ,一雙曲線的頂點是該橢圓的焦點,且它的實軸長等于虛軸長,設
,一雙曲線的頂點是該橢圓的焦點,且它的實軸長等于虛軸長,設![]() 為該雙曲線上異于頂點的任一點,直線
為該雙曲線上異于頂點的任一點,直線![]() 和
和![]() 與橢圓的交點分別為
與橢圓的交點分別為![]() 和
和![]() ,其中
,其中![]() 在
在![]() 軸的同一側.
軸的同一側.
(1)求橢圓和雙曲線的標準方程;
(2)是否存在題設中的點![]() ,使得
,使得![]() ?若存在, 求出點
?若存在, 求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com