日本三级国产,看毛片网,男人久久天堂

精英家教網 > 高中數學 > 題目詳情

【題目】如圖，已知雙曲線 =1（a＞0，b＞0）的左右焦點分別為F1 ， F2 ， |F1F2|=4，P是雙曲線右支上的一點，F2P與y軸交于點A，△APF1的內切圓在邊PF1上的切點為Q，若|PQ|=1，則雙曲線的離心率是（）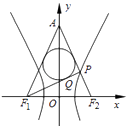
A.3
B.2
C.
D.

【答案】B
【解析】解：由題意，∵|PQ|=1，△APF1的內切圓在邊PF1上的切點為Q， ∴根據切線長定理可得AM=AN，F1M=F1Q，PN=PQ，
∵|AF1|=|AF2|，
∴AM+F1M=AN+PN+NF2 ，
∴F1M=PN+NF2=PQ+PF2
∴|PF1|﹣|PF2|=F1Q+PQ﹣PF2=F1M+PQ﹣PF2=PQ+PF2+PQ﹣PF2=2PQ=2，
∵|F1F2|=4，
∴雙曲線的離心率是e= =2．
故選：B．

由|PQ|=1，△APF1的內切圓在邊PF1上的切點為Q，根據切線長定理，可得|PF1|﹣|PF2|=2，結合|F1F2|=4，即可得出結論．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】已知直線l的參數方程為（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，圓C的極坐標方程為ρ=4sin（θ﹣ ）．
（1）求圓C的直角坐標方程；
（2）若P（x，y）是直線l與圓面ρ≤4sin（θ﹣ ）的公共點，求 x+y的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】設數列{an}的前n項和為Sn ，且Sn=2﹣an ， n∈N* ，設函數f（x）=log x，數列{bn}滿足bn=f（an），記{bn}的前n項和為Tn ．（Ⅰ）求an及Tn；
（Ⅱ）記cn=anbn ，求cn的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=lnx﹣ax2﹣bx（a，b∈R），g（x）= ﹣lnx．
（1）當a=﹣1時，f（x）與g（x）在定義域上的單調性相反，求b的取值范圍；
（2）當a，b都為0時，斜率為k的直線與曲線y=f（x）交A（x1 ， y1），B（x2 ， y2）（x1＜x2）于兩點，求證：x1＜．