
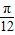 ,
, ],求f(x)的值域.
],求f(x)的值域.
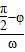 =
=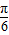 可求得φ;
可求得φ; =kπ+
=kπ+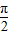 可求其對稱軸方程,由2x+
可求其對稱軸方程,由2x+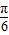 =kπ可求其對稱中心坐標;
=kπ可求其對稱中心坐標;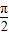 ≤2x+
≤2x+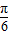 ≤2kπ+
≤2kπ+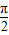 ,k∈Z可得f(x)的單調增區間;
,k∈Z可得f(x)的單調增區間; ≤2x+
≤2x+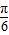 ≤2kπ+
≤2kπ+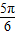 ,k∈Z,可求使f(x)≥1 成立的x 的取值集合;
,k∈Z,可求使f(x)≥1 成立的x 的取值集合;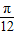 ,
, ],2x+
],2x+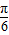 ∈[
∈[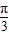 ,
,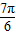 ],從而可求求f(x)的值域.
],從而可求求f(x)的值域.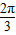 -
-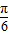 )=π=
)=π=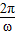 ,
, =
=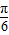 ,
,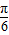 (5分)
(5分)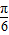 )(6分)
)(6分)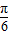 =kπ+
=kπ+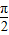 ,k∈Z得其對稱軸方程為:x=
,k∈Z得其對稱軸方程為:x=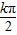 +
+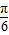 ,k∈Z;對稱中心坐標為:(
,k∈Z;對稱中心坐標為:(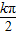 -
-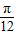 ,);
,);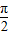 ≤2x+
≤2x+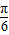 ≤2kπ+
≤2kπ+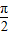 ,k∈Z得:(8分)
,k∈Z得:(8分)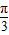 ≤x≤kπ+
≤x≤kπ+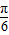 ,k∈Z(9分)
,k∈Z(9分)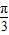 ,kπ+
,kπ+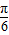 ],(k∈Z)(10分)
],(k∈Z)(10分)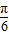 )≥1,
)≥1,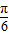 )≥
)≥ ,
,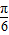 ≤2x+
≤2x+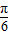 ≤2kπ+
≤2kπ+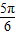 ,k∈Z,
,k∈Z,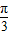 ,k∈Z,
,k∈Z,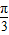 ,k∈Z}(12分)
,k∈Z}(12分)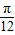 ,
,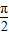 ],
],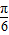 ∈[
∈[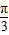 ,
,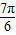 ].
].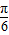 =
=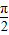 ,即x=
,即x=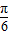 時,f(x)取得最大值2;
時,f(x)取得最大值2;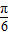 =
=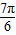 ,即x=
,即x=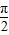 時,f(x)取得最小值-1,故f(x)的值域為[-1,2].
時,f(x)取得最小值-1,故f(x)的值域為[-1,2].

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:
 已知如圖是函數f(x)=Asin(ωx+φ)(A>0,ω>0)的部分圖象
已知如圖是函數f(x)=Asin(ωx+φ)(A>0,ω>0)的部分圖象| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知如圖是函數f(x)=Asin(ωx+φ)(A>0,ω>0)的部分圖象.
已知如圖是函數f(x)=Asin(ωx+φ)(A>0,ω>0)的部分圖象.| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年新疆巴州尉犁中學高三(上)第二次月考數學試卷(解析版) 題型:解答題
 ,
, ],求f(x)的值域.
],求f(x)的值域.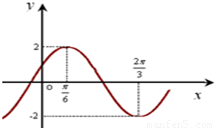
查看答案和解析>>
科目:高中數學 來源:2012-2013學年新疆烏魯木齊一中高三(上)第一次月考數學試卷(文科)(解析版) 題型:解答題
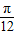 ,
,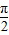 ],求f(x)的值域.
],求f(x)的值域.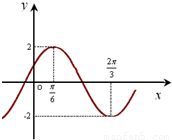
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com