
【題目】設函數![]() ,其中
,其中![]()
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)若![]() 存在極值點
存在極值點![]() ,且
,且![]() ,其中
,其中![]() ,求證:
,求證: ![]() ;
;
(Ⅲ)設![]() ,函數
,函數![]() ,求證:
,求證: ![]() 在區間
在區間![]() 上最大值不小于
上最大值不小于![]() .
.
【答案】(Ⅰ)見解析;(Ⅱ)見解析;(Ⅲ)見解析.
【解析】試題分析:(1)求單調區間,先求導解導數大于零求遞增區間,導數小于零求遞減區間,但要注意a的取值對導數符號得影響(2)函數存在極值點,即將![]() 代入導函數等于零,又
代入導函數等于零,又![]() 所以
所以![]() 從而得證(3)求最值先分析函數單調性即可,然后討論在區間
從而得證(3)求最值先分析函數單調性即可,然后討論在區間![]() 得極值和端點值大小來確定最大值,再驗證其不小于
得極值和端點值大小來確定最大值,再驗證其不小于![]() 即可
即可
試題解析:
(Ⅰ)由![]() ,可得
,可得![]() ,
,
下面分兩種情況討論:
(1)當![]() 時,有
時,有![]() 恒成立,所以
恒成立,所以![]() 單調遞增區間為
單調遞增區間為![]()
(2)當![]() 時,令
時,令![]() ,解得
,解得![]() ,或
,或![]() ,
,
當![]() 變化時,
變化時, ![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 單調遞增 | 極大值 | 單調遞減 | 極小值 | 單調遞增 |
所以![]() 的單調遞減區間為
的單調遞減區間為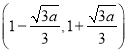 ,單調遞增區間為
,單調遞增區間為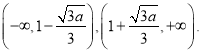
(Ⅱ)證明:因為![]() 存在極值點,所以由(Ⅰ)知
存在極值點,所以由(Ⅰ)知![]() ,且
,且![]() ,由題意,得
,由題意,得![]() ,即
,即![]()
進而![]()
又![]()
![]() ,且
,且![]() ,由題意及(Ⅰ)知,存在唯一實數
,由題意及(Ⅰ)知,存在唯一實數![]() 滿足
滿足![]() ,且
,且![]() ,因此
,因此![]() ,所以
,所以![]() ;
;
(Ⅲ)證明:設![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,
, ![]() 表示
表示![]() 兩數的最大值,下面分三種情況討論:
兩數的最大值,下面分三種情況討論:
(1)當![]() 時,
時, ![]() ,由(Ⅰ)知,
,由(Ⅰ)知, ![]() 在區間
在區間![]() 上單調遞減,所以
上單調遞減,所以![]() 在區間
在區間![]() 上的取值范圍為
上的取值范圍為![]() ,因此
,因此
![]()
![]()

所以![]()
(2)當![]() 時,
時, ![]() ,由(Ⅰ)和(Ⅱ)知,
,由(Ⅰ)和(Ⅱ)知, 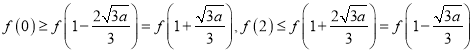 ,
,
所以![]() 在區間
在區間![]() 上的取值范圍為
上的取值范圍為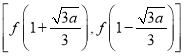 ,
,
因此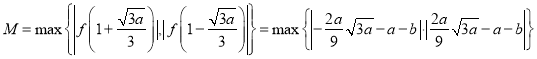
![]()
![]()
(3)當時![]() 時,
時, ![]() ,由(Ⅰ)和(Ⅱ)知,
,由(Ⅰ)和(Ⅱ)知, 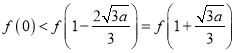 ,
, 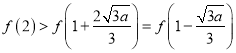 ,
,
所以![]() 在區間
在區間![]() 上的取值范圍為
上的取值范圍為![]() ,因此
,因此![]() ,
,
綜上所述,當![]() 時,
時, ![]() 在區間
在區間![]() 上的最大值不小于
上的最大值不小于![]() .
.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 上是增函數,求實數
上是增函數,求實數![]() 的取值范圍;
的取值范圍;
(2)求所有的實數![]() ,使得對任意
,使得對任意![]() 時,函數
時,函數![]() 的圖象恒在函數
的圖象恒在函數![]() 圖象的下方;
圖象的下方;
(3)若存在![]() ,使得關于
,使得關于![]() 的方程
的方程![]() 有三個不相等的實數根,求實數
有三個不相等的實數根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖.
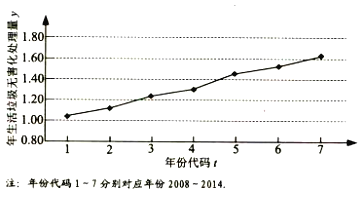
(Ⅰ)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(Ⅱ)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測2016年我國生活垃圾無害化處理量.
的回歸方程(系數精確到0.01),預測2016年我國生活垃圾無害化處理量.
參考數據: ![]() ,
, ![]() ,
, 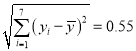 ,
, ![]() .
.
參考公式:相關系數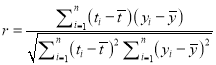 ,
,
回歸方程![]() ,
, 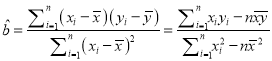 ,
,
本題中斜率和截距的最小二乘估計公式分別為: 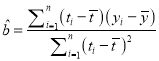 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1在![]() △
△![]() 中,
中,![]()
![]() ,
,![]() 、
、![]() 分別為線段
分別為線段![]() 、
、![]() 的中點,
的中點,![]() ,
,![]() .以
.以![]() 為折痕,將
為折痕,將![]() △
△![]() 折起到圖2的位置,使平面
折起到圖2的位置,使平面![]() ⊥平面
⊥平面![]() ,連接
,連接![]() ,
,![]() ,設
,設![]() 是線段
是線段![]() 上的動點,滿足
上的動點,滿足![]() .
.
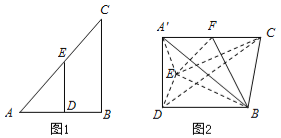
(1)證明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位從一所學校招收某類特殊人才,對20位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
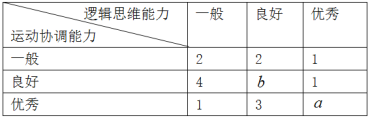
例如表中運動協調能力良好且邏輯思維能力一般的學生是4人,由于部分數據丟失,只知道從這20位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)從運動協調能力為優秀的學生中任意抽取2位,求其中至少有一位邏輯思維能力優秀的學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]()
若![]() ,過點
,過點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程;
的方程;
若曲線![]() 表示圓,且直線
表示圓,且直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得以
,使得以![]() 為直徑的圓過原點,若存在,求出實數
為直徑的圓過原點,若存在,求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的方程為
的方程為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上到直線
上到直線![]() 距離最小的點,點
距離最小的點,點![]() 是拋物線上異于點
是拋物線上異于點![]() 的點,直線
的點,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,過點
,過點![]() 與
與![]() 軸平行的直線與拋物線
軸平行的直線與拋物線![]() 交于點
交于點![]() .
.
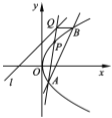
(Ⅰ)求點![]() 的坐標;
的坐標;
(Ⅱ)證明直線![]() 恒過定點,并求這個定點的坐標.
恒過定點,并求這個定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布圖中![]() 的值,并估計該企業的職工對該部門評分不低于80的概率;
的值,并估計該企業的職工對該部門評分不低于80的概率;
(2)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率..
的概率..
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com