
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,且過點
,且過點![]() .
.
(1)求C的方程;
(2)若直線l與C有且只有一個公共點,l與圓x2+y2=6交于A,B兩點,直線OA,OB的斜率分別記為k1,k2.試判斷k1k2是否為定值,若是,求出該定值;否則,請說明理由.
【答案】(1)![]() ;(2)k1k2為定值
;(2)k1k2為定值![]() .
.
【解析】
(1)由題意可得關于a,b,c的方程組,求解a,b,c的值,即可得到橢圓的方程;
(2)①當過點P的直線斜率不存在時,直線的方程為x=±2,求得![]() ,②當過P的直線斜率存在時,設其方程為y=kx+m,聯立直線方程與橢圓方程,由判別式等于0可得m2=4k2+2,聯立直線方程與橢圓方程,利用根與系數的關系結合斜率公式可得
,②當過P的直線斜率存在時,設其方程為y=kx+m,聯立直線方程與橢圓方程,由判別式等于0可得m2=4k2+2,聯立直線方程與橢圓方程,利用根與系數的關系結合斜率公式可得![]() 為定值
為定值![]() .
.
(1)由題意,得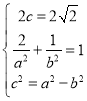 ,
,
解得![]() .
.
∴橢圓C的方程為![]() .
.
(2)k1k2為定值![]()
理由如下:
①當過點P的直線斜率不存在時,直線的方程為x=±2;
當x=2時,![]() ,則
,則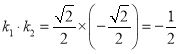 ,
,
當![]() 時,
時,![]() ,則
,則![]() .
.
②當過P的直線斜率存在時,設其方程為![]() ,
,
聯立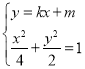 ,得
,得![]()
由題意![]() ,得
,得![]() ,
,
聯立![]() ,得
,得![]()
則![]()
所以![]()
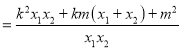
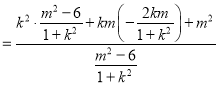
![]()
![]()
綜上,![]() 為定值
為定值![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的方程
的方程![]() ,焦點為
,焦點為![]() ,已知點
,已知點![]() 在
在![]() 上,且點
上,且點![]() 到點
到點![]() 的距離比它到
的距離比它到![]() 軸的距離大1.
軸的距離大1.
(1)試求出拋物線![]() 的方程;
的方程;
(2)若拋物線![]() 上存在兩動點
上存在兩動點![]() (
(![]() 在對稱軸兩側),滿足
在對稱軸兩側),滿足![]() (
(![]() 為坐標原點),過點
為坐標原點),過點![]() 作直線交
作直線交![]() 于
于![]() 兩點,若
兩點,若![]() ,線段
,線段![]() 上是否存在定點
上是否存在定點![]() ,使得
,使得![]() 恒成立?若存在,請求出
恒成立?若存在,請求出![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知在算法中“![]() ”和“
”和“![]() ”分別表示取商和取余數.為了驗證三位數卡普雷卡爾“數字黑洞”(即輸入一個無重復數字的三位數,經過如圖的有限次的重排求差計算,結果都為495).小明輸入
”分別表示取商和取余數.為了驗證三位數卡普雷卡爾“數字黑洞”(即輸入一個無重復數字的三位數,經過如圖的有限次的重排求差計算,結果都為495).小明輸入![]() ,則輸出的
,則輸出的![]() ( )
( )![]()
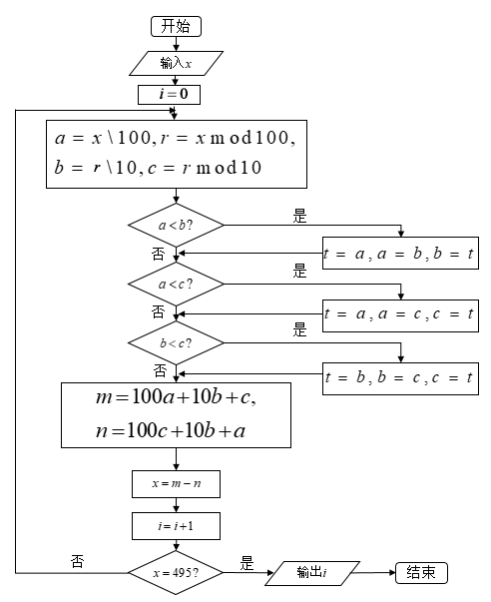
A.3B.4C.5D.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2021年開始,我省將試行“3+1+2“的普通高考新模式,即除語文、數學、外語3門必選科目外,考生再從物理、歷史中選1門,從化學、生物、地理、政治中選2門作為選考科目.為了幫助學生合理選科,某中學將高一每個學生的六門科目綜合成績按比例均縮放成5分制,繪制成雷達圖.甲同學的成績雷達圖如圖所示,下面敘述一定不正確的是( )

A.甲的物理成績領先年級平均分最多
B.甲有2個科目的成績低于年級平均分
C.甲的成績從高到低的前3個科目依次是地理、化學、歷史
D.對甲而言,物理、化學、地理是比較理想的一種選科結果
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{![]() }的首項a1=2,前n項和為
}的首項a1=2,前n項和為![]() ,且數列{
,且數列{![]() }是以
}是以![]() 為公差的等差數列·
為公差的等差數列·
(1)求數列{![]() }的通項公式;
}的通項公式;
(2)設![]() ,
,![]() ,數列{
,數列{![]() }的前n項和為
}的前n項和為![]() ,
,
①求證:數列{![]() }為等比數列,
}為等比數列,
②若存在整數m,n(m>n>1),使得![]() ,其中
,其中![]() 為常數,且
為常數,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩個快遞公司的工作狀況,假設同一個公司快遞員的工作狀況基本相同,現從甲、乙兩公司各隨機抽取一名快遞員,并從兩人某月(30天)的快遞件數記錄結果中隨機抽取10天的數據,制表如圖:

每名快遞員完成一件貨物投遞可獲得的勞務費情況如下:甲公司規定每件4.5元;乙公司規定每天35件以內(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根據表中數據寫出甲公司員工A在這10天投遞的快遞件數的平均數和眾數;
(2)為了解乙公司員工B的每天所得勞務費的情況,從這10天中隨機抽取1天,他所得的勞務費記為X(單位:元),求X的分布列和數學期望;
(3)根據表中數據估算兩公司的每位員工在該月所得的勞務費.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com