
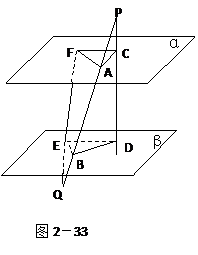
 如圖2-33:線段PQ分別交兩個平行平面α、β于A、B兩點,線段PD分別交α、β于C、D兩點,線段QF分別交α、β于F、E兩點,若PA=9,AB=12,BQ=12,
如圖2-33:線段PQ分別交兩個平行平面α、β于A、B兩點,線段PD分別交α、β于C、D兩點,線段QF分別交α、β于F、E兩點,若PA=9,AB=12,BQ=12,![]() ACF的面積為72,求
ACF的面積為72,求![]() BDE的面積。
BDE的面積。
求![]() BDE的面積,看起來似乎與本節內容無關,事實上,已知
BDE的面積,看起來似乎與本節內容無關,事實上,已知![]() ACF的面積,若
ACF的面積,若![]() BDE與
BDE與![]() ACF的對應邊有聯系的話,可以利用
ACF的對應邊有聯系的話,可以利用![]() ACF的面積求出
ACF的面積求出![]() BDE的面積。
BDE的面積。
(提示:①![]() ABC的兩條鄰邊分別長為a、b,夾角為θ,則
ABC的兩條鄰邊分別長為a、b,夾角為θ,則![]() ABC的面積S=
ABC的面積S=![]() absinθ,②sinα=sin(180°-α)
absinθ,②sinα=sin(180°-α)
∵平面QAF∩α=AF,平面QAF∩β=BE,又∵α∥β,∴AF∥BE
同理可證:AC//BD,∴∠FAC與∠EBD相等或互補,即sin∠FAC= sin∠EBD.
由 AF∥BE,得![]() ,∴BE=
,∴BE=![]() AF
AF
由BD//AC,得:![]() ,∴BD=
,∴BD=![]() AC
AC
又∵![]() ACF的面積為72,即
ACF的面積為72,即![]() AF·AC·sin∠FAC=72,
AF·AC·sin∠FAC=72,
∴![]() =
=![]() BE·BD·sin∠EBD
BE·BD·sin∠EBD
=![]() ·
·![]() AF·
AF·![]() AC·sin∠FAC
AC·sin∠FAC
=![]() ·
·![]() AF·AC·sin∠FAC=
AF·AC·sin∠FAC=![]() ×72=84
×72=84
∴![]() BDE的面積為84平方單位。
BDE的面積為84平方單位。


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
 (2012•湖南)函數f(x)=sin (ωx+φ)的導函數y=f′(x)的部分圖象如圖所示,其中,P為圖象與y軸的交點,A,C為圖象與x軸的兩個交點,B為圖象的最低點.
(2012•湖南)函數f(x)=sin (ωx+φ)的導函數y=f′(x)的部分圖象如圖所示,其中,P為圖象與y軸的交點,A,C為圖象與x軸的兩個交點,B為圖象的最低點.| π |
| 6 |
3
| ||
| 2 |
 |
| ABC |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
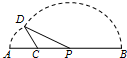 如圖,線段AB=8,點C在線段AB上,且AC=2,P為線段CB上一動點,點A繞點C旋轉后與點B繞點P旋轉后重合于點D.設CP=x,△CPD的面積為f(x).則f(x)的最大值為( )
如圖,線段AB=8,點C在線段AB上,且AC=2,P為線段CB上一動點,點A繞點C旋轉后與點B繞點P旋轉后重合于點D.設CP=x,△CPD的面積為f(x).則f(x)的最大值為( )查看答案和解析>>
科目:高中數學 來源: 題型:
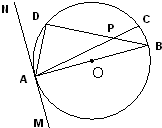 (幾何證明選講)如圖,半徑是3
(幾何證明選講)如圖,半徑是3| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com