
 如圖,正四棱錐P-ABCD中底面邊長為2$\sqrt{2}$,側棱PA與底面ABCD所成角的正切值為$\frac{{\sqrt{6}}}{2}$.
如圖,正四棱錐P-ABCD中底面邊長為2$\sqrt{2}$,側棱PA與底面ABCD所成角的正切值為$\frac{{\sqrt{6}}}{2}$.分析 (1)連結AC,BD交于點O,連結PO,則PO⊥面ABCD,利用側棱PA與底面ABCD所成角的正切值為$\frac{{\sqrt{6}}}{2}$,可得PO=$\sqrt{6}$,利用勾股定理建立方程,求出R;
(2)容易證明以EO$\stackrel{∥}{=}$$\frac{1}{2}PD$.可得∠AEO就是異面直線PD與AE所成的角,在Rt△AOE中求解
解答  解:(1)連結AC,BD交于點O,連結PO,則PO⊥面ABCD,
解:(1)連結AC,BD交于點O,連結PO,則PO⊥面ABCD,
∴∠PAO就是PA與底面ABCD所成的角,
∴tan∠PAO=$\frac{{\sqrt{6}}}{2}$.
又AB=2$\sqrt{2}$,則PO=AO•tan∠PAO=$\sqrt{6}$.
設F為外接球球心,連FA,
易知FA=FP,設FO=x,則
x2+4=($\sqrt{6}$-x)2,
∴x=$\frac{\sqrt{6}}{6}$,
∴正四棱錐P-ABCD的外接球半徑為$\frac{5\sqrt{6}}{6}$;
(2)連結EO,由于O為BD中點,E為PD中點,所以EO$\stackrel{∥}{=}$$\frac{1}{2}PD$.
∴∠AEO就是異面直線PD與AE所成的角.
在Rt△POD中,$PD=\sqrt{O{D^2}+P{O^2}}=\frac{{\sqrt{5}}}{2}$.
∴$EO=\frac{{\sqrt{5}}}{4}$.
由AO⊥BD,AO⊥PO可知AO⊥面PBD.
所以AO⊥EO,
在Rt△OAE中,tan∠AEO=$\frac{AO}{EO}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{5}}{4}}$=$\frac{2\sqrt{10}}{5}$,
即異面直線PD與AE所成角的正切值為$\frac{{2\sqrt{10}}}{5}$.
點評 本題考查正四棱錐P-ABCD的外接球的表面積,考查學生的計算能力,正確求出正四棱錐P-ABCD的外接球的半徑是關鍵.


 優百分課時互動系列答案
優百分課時互動系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 數學 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 92 | 72 | 93 |
| 物理 | 90 | 63 | 72 | 92 | 91 | 71 | 58 | 91 | 93 | 81 | 77 | 82 | 48 | 91 | 69 | 96 | 61 | 84 | 78 | 93 |
 | 優秀 | 不優秀 | 合計 |
| 優秀 | 6 | 2 | 8 |
| 不優秀 | 2 | 10 | 12 |
| 合計 | 8 | 12 | 20 |
| P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
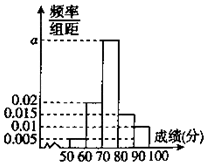 為了了解某學校高二年級學生的物理成績,從中抽取n名學生的物理成績(百分制)作為樣本,按成績分成 5組:[50,60),[60,70),[70,80),[80,90),[90,100],頻率分布直方圖如圖所示,成績落在[70,80)中的人數為20.
為了了解某學校高二年級學生的物理成績,從中抽取n名學生的物理成績(百分制)作為樣本,按成績分成 5組:[50,60),[60,70),[70,80),[80,90),[90,100],頻率分布直方圖如圖所示,成績落在[70,80)中的人數為20.| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合計 | |
| 優秀 | |||
| 不優秀 | |||
| 合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1] | B. | [-1,0) | C. | [-1,0] | D. | (-∞,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=x-3 | B. | y=-2x+1 | C. | y=2x-4 | D. | y=-2x-3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com