
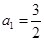 ,公差
,公差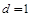 ,求滿足
,求滿足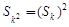 的正整數k;
的正整數k;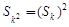 成立
成立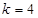 (Ⅱ)見解析
(Ⅱ)見解析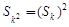 成立”這句話將k取兩個特殊值確定出等差數列的首項和公差,但沒有認識到求解出的等差數列僅是對已知條件成立的必要條件,但不是條件成立的充分條件。還應進一步的由特殊到一般。
成立”這句話將k取兩個特殊值確定出等差數列的首項和公差,但沒有認識到求解出的等差數列僅是對已知條件成立的必要條件,但不是條件成立的充分條件。還應進一步的由特殊到一般。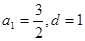 時
時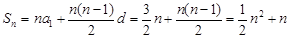
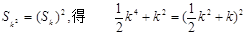 ,即
,即 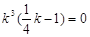 又
又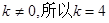 .
.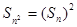 中分別取k=1,2,得
中分別取k=1,2,得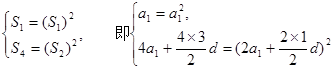
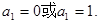 當
當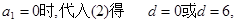
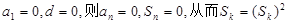 成立 ,
成立 ,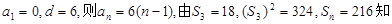
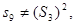 故所
故所
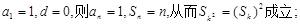
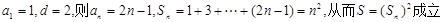 .
.

 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源:不詳 題型:解答題
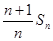
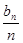 的最小值.
的最小值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com