
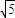 ,
,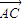 •
•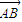 =5.
=5.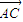 •
•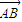 =5,
=5,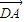 +
+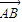 =
=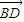 ,利用平方求出AD,再求AC的長;
,利用平方求出AD,再求AC的長;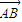 •
•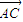 =5,AB=3,AC=2AD.
=5,AB=3,AC=2AD.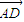 •
• =
= .
.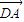 +
+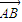 =
=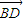 ,∴(
,∴(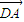 +
+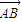 )2=
)2=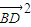 .
.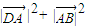 -2
-2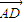 •
•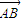 =|
=|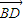 |2,
|2,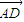 •
• =
= .可得cosA=
.可得cosA= ,∴sinA=
,∴sinA=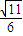 .
.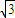 .
.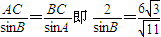 可得sinB=
可得sinB=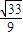 ,∴cosB=
,∴cosB= .
.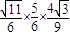 -(1-2×
-(1-2×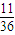 )×
)×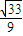 =
=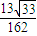 .
.

 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案 黃岡創優卷系列答案
黃岡創優卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com