函數f(x)的定義域為{x|x∈R,且x≠1},已知f(x+1)為奇函數,當x<1時,f(x)=2x2-x+1,則當x>1時,f(x)的遞減區間是
【答案】
分析:由f(x+1)為奇函數,利用換元法得f(x)=-f(2-x),再設x>1,則2-x<1,代入解析式求出f(2-x),由關系式求出
f(x),根據二次函數的單調性求出它的減區間.
解答:解:由題意知,f(x+1)為奇函數,則f(-x+1)=-f(x+1),
令t=-x+1,則x=1-t,故f(t)=-f(2-t),即f(x)=-f(2-x),
設x>1,則2-x<1,
∵當x<1時,f(x)=2x
2-x+1,∴f(2-x)=2(2-x)
2-(2-x)+1=2x
2-7x+7,
∴f(x)=-f(2-x)=-2x
2+7x-7,∴函數的對稱軸x=

故所求的減區間是
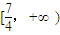
.
故答案為:
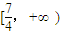
.
點評:本題主要考查對單調性和奇偶性的理解,判斷函數奇偶性和求函數單調區間的基本方法以及函數解析式的求解方法的掌握,關鍵利用奇函數的定義推出的關系式;并且函數的單調性、奇偶性是高考函數題的重點考查內容.


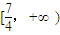 .
.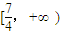 .
.

 同步練習強化拓展系列答案
同步練習強化拓展系列答案