
【題目】已知點![]() 和點
和點![]() .
.
(Ⅰ)求線段![]() 的垂直平分線的直線方程;
的垂直平分線的直線方程;
(Ⅱ)若直線![]() 過點
過點![]() ,且
,且![]() ,
,![]() 到直線
到直線![]() 的距離相等.求直線
的距離相等.求直線![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)先根據中點坐標公式求出線段![]() 的中點坐標,再根據斜率公式求出直線
的中點坐標,再根據斜率公式求出直線![]() 的斜率,再根據互相垂直的直線斜率之間的關系求出直線
的斜率,再根據互相垂直的直線斜率之間的關系求出直線![]() 的垂線的斜率,最后利用直線點斜式方程進行求解即可;
的垂線的斜率,最后利用直線點斜式方程進行求解即可;
(Ⅱ)根據直線![]() 是否存在斜率分類討論求解.當直線
是否存在斜率分類討論求解.當直線![]() 存在斜率時,根據題意結合點到直線距離公式進行求解,當直線
存在斜率時,根據題意結合點到直線距離公式進行求解,當直線![]() 不存在斜率時,寫出直線方程,然后進行判斷是否符合題意即可.
不存在斜率時,寫出直線方程,然后進行判斷是否符合題意即可.
(Ⅰ)因為點![]() 和點
和點![]() .所以線段
.所以線段![]() 的中點
的中點![]() 坐標為:
坐標為:
![]() ,即
,即![]() ,
,
直線![]() 的斜率為:
的斜率為:![]() ,
,
因此直線![]() 的垂線的斜率為:
的垂線的斜率為: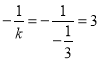 ,
,
因此線段![]() 的垂直平分線的直線方程為:
的垂直平分線的直線方程為:![]() ,
,
化簡得:![]() ;
;
(Ⅱ)設直線![]() 存在斜率,設為
存在斜率,設為![]() ,
,
因為直線![]() 過點
過點![]() ,所以直線
,所以直線![]() 的方程為:
的方程為:![]() ,
,
又因為![]() ,
,![]() 到直線
到直線![]() 的距離相等,所以有
的距離相等,所以有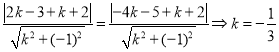 ,
,
即![]() ;
;
當直線![]() 不存在斜率,因為直線
不存在斜率,因為直線![]() 過點
過點![]() ,所以直線
,所以直線![]() 的方程為:
的方程為:![]() ,
,
因為點![]() 和點
和點![]() 到直線
到直線![]() 的距離都是3,所以符合題意.
的距離都是3,所以符合題意.
因此直線![]() 的方程為:
的方程為:![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】為了解戶籍、性別對生育二胎選擇傾向的影響,某地從育齡人群中隨機抽取了容量為![]() 的調查樣本,其中城鎮戶籍與農村戶籍各
的調查樣本,其中城鎮戶籍與農村戶籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人,繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例圖(如圖所示),其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述中錯誤的是( )
人,繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例圖(如圖所示),其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述中錯誤的是( )
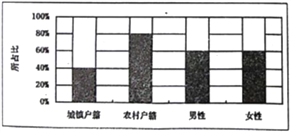
A. 是否傾向選擇生育二胎與戶籍有關
B. 是否傾向選擇生育二胎與性別有關
C. 傾向選擇生育二胎的人員中,男性人數與女性人數相同
D. 傾向選擇不生育二胎的人員中,農村戶籍人數少于城鎮戶籍人數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() 的定義域為R,則實數m取值范圍為
的定義域為R,則實數m取值范圍為
A.{m|–1≤m≤0}B.{m|–1<m<0}
C.{m|m≤0}D.{m|m<–1或m>0}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,
兩點,![]() 是圓
是圓![]() 上不同于
上不同于![]() 兩點的動點,求
兩點的動點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個四位數的各位數字相加和為![]() ,則稱該數為“完美四位數”,如數字“
,則稱該數為“完美四位數”,如數字“![]() ”.試問用數字
”.試問用數字![]() 組成的無重復數字且大于
組成的無重復數字且大于![]() 的“完美四位數”有( )個
的“完美四位數”有( )個
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各進行![]() 次射擊,甲每次擊中目標的概率為
次射擊,甲每次擊中目標的概率為![]() ,乙每次擊中目標的概率
,乙每次擊中目標的概率![]() ,
,
(Ⅰ)記甲擊中目標的次數為![]() ,求
,求![]() 的概率分布及數學期望;
的概率分布及數學期望;
(Ⅱ)求甲恰好比乙多擊中目標![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市為調查會員某年度上半年的消費情況制作了有獎調查問卷發放給所有會員,并從參與調查的會員中隨機抽取![]() 名了解情況并給予物質獎勵.調查發現抽取的
名了解情況并給予物質獎勵.調查發現抽取的![]() 名會員消費金額(單位:萬元)都在區間
名會員消費金額(單位:萬元)都在區間![]() 內,調查結果按消費金額分成
內,調查結果按消費金額分成![]() 組,制作成如下的頻率分布直方圖.
組,制作成如下的頻率分布直方圖.

(1)求該![]() 名會員上半年消費金額的平均值與中位數;(以各區間的中點值代表該區間的均值)
名會員上半年消費金額的平均值與中位數;(以各區間的中點值代表該區間的均值)
(2)若再從這![]() 名會員中選出一名會員參加幸運大抽獎,幸運大抽獎方案如下:會員最多有兩次抽獎機會,每次抽獎的中獎概率均為
名會員中選出一名會員參加幸運大抽獎,幸運大抽獎方案如下:會員最多有兩次抽獎機會,每次抽獎的中獎概率均為![]() ,第一次抽獎,若未中獎,則抽獎結束.若中獎,則通過拋擲一枚質地均勻的硬幣,決定是否繼續進行第二次抽獎.規定:拋出的硬幣,若反面朝上,則會員獲得
,第一次抽獎,若未中獎,則抽獎結束.若中獎,則通過拋擲一枚質地均勻的硬幣,決定是否繼續進行第二次抽獎.規定:拋出的硬幣,若反面朝上,則會員獲得![]() 元獎金,不進行第二次抽獎;若正面朝上,會員需進行第二次抽獎,且在第二次抽獎中,如果中獎,則獲得獎金
元獎金,不進行第二次抽獎;若正面朝上,會員需進行第二次抽獎,且在第二次抽獎中,如果中獎,則獲得獎金![]() 元,如果未中獎,則所獲得的獎金為
元,如果未中獎,則所獲得的獎金為![]() 元.若參加幸運大抽獎的會員所獲獎金(單位:元)用
元.若參加幸運大抽獎的會員所獲獎金(單位:元)用![]() 表示,求
表示,求![]() 的分布列與期望值
的分布列與期望值![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com