【題目】已知定義在
上的函數
，
為其導數，且
恒成立，則（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
通過
，可以聯想到導數運算的除法，這樣可以構造新函數
，
，這樣就可以判斷出函數
在
上的單調性，把四個選項變形，利用單調性判斷出是否正確.
通過,這個結構形式，可以構造新函數，
，而，所以當時，
，所以函數在上是單調遞增函數，現對四個選項逐一判斷：
選項A. 
,可以判斷
是否正確，
也就是判斷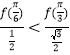
是否正確，即判斷
是否成立，因為
，在上是單調遞增函數，所以有，故選項A正確；
選項B.
，也就是判斷
是否正確，即判斷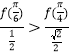
是否成立，即判斷
是否成立，因為
，在上是單調遞增函數，所以有
，故選項B不正確；
選項C. 
，也就是判斷
是否正確，即判斷
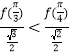是否成立，即判斷
是否成立，因為
，在上是單調遞增函數，所以有
，故選項C不正確；
選項D.
，也就是判斷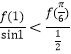
，是否成立，即判斷
是否成立，因為
，在上是單調遞增函數，所以有
，因此選項D不正確，故本題選A.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知
，
，其中
為實常數.
（1）若函數
在區間[2，3]上為單調遞增函數，求的取值范圍；
（2）高函數
在區間
上的最小值為
，試討論函數
，
的零點的情況.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現需要設計一個倉庫，它由上下兩部分組成，上部分的形狀是正四棱錐
，下部分的形狀是正四棱柱
（如圖所示），并要求正四棱柱的高
是正四棱錐的高
的4倍.
（1）若
則倉庫的容積是多少？
（2）若正四棱錐的側棱長為
，則當為多少時，倉庫的容積最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
在直角坐標系
中，直線
的參數方程為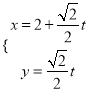
（
為參數），以原點為極點， 
軸的正半軸為極軸，以相同的長度單位建立極坐標系，曲線
的極坐標方程為
.
（Ⅰ）求直線
的極坐標方程和曲線
的直角坐標方程；
（Ⅱ）已知
，直線
與曲線
交于
， 
兩點，若
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地植被面積 
（公頃）與當地氣溫下降的度數
（
）之間有如下的對應數據：
| 20 | 40 | 50 | 60 | 80 |
| 3 | 4 | 4 | 4 | 5 |
（1）請用最小二乘法求出關于的線性回歸方程
；
（2）根據（1）中所求線性回歸方程，如果植被面積為200公頃，那么下降的氣溫大約是多少？
參考公式:用最小二乘法求線性回歸方程系數公式：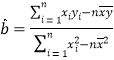
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過圓
與
軸正半軸的交點A作圓O的切線
，M為上任意一點，過M作圓O的另一條切線，切點為Q．當點M在直線上運動時，△MAQ的垂心的軌跡方程為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知直線l：
－y＋3＋
＝0和圓
：
＋
＋8x＋F＝0．若直線l被圓截得的弦長為
．
（1）求圓的方程；
（2）設圓和x軸相交于A，B兩點，點P為圓上不同于A，B的任意一點，直線PA，PB交y軸于M，N兩點．當點P變化時，以MN為直徑的圓
是否經過圓內一定點？請證明你的結論；
（3）若△RST的頂點R在直線x＝－1上，點S，T在圓上，且直線RS過圓心，∠SRT＝
，求點R的縱坐標的范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
