
【題目】某實驗室一天的溫度(單位:℃)隨時間t(單位:h)的變化近似滿足函數關系: f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(Ⅰ)求實驗室這一天的最大溫差;
(Ⅱ)若要求實驗室溫度不高于11℃,則在哪段時間實驗室需要降溫?
【答案】解:(Ⅰ)∵f(t)=10﹣ ![]() =10﹣2sin(
=10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24), ∴
),t∈[0,24), ∴ ![]() ≤
≤ ![]() t+
t+ ![]() <
< ![]() ,故當
,故當 ![]() t+
t+ ![]() =
= ![]() 時,及t=14時,函數取得最大值為10+2=12,
時,及t=14時,函數取得最大值為10+2=12,
當 ![]() t+
t+ ![]() =
= ![]() 時,即t=2時,函數取得最小值為10﹣2=8,
時,即t=2時,函數取得最小值為10﹣2=8,
故實驗室這一天的最大溫差為12﹣8=4℃.
(Ⅱ)由題意可得,當f(t)>11時,需要降溫,由(Ⅰ)可得f(t)=10﹣2sin( ![]() t+
t+ ![]() ),
),
由10﹣2sin( ![]() t+
t+ ![]() )>11,求得sin(
)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,
,
解得10<t<18,即在10時到18時,需要降溫.
【解析】(Ⅰ)利用兩角和差的正弦公式化簡函數解析式為f(t)10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),利用正弦函數的定義域和值域求得f(x)的最大值及最小值,可得實驗室這一天的最大溫差.(Ⅱ)由題意可得,當f(t)>11時,需要降溫,由f(t)>11,求得sin(
),t∈[0,24),利用正弦函數的定義域和值域求得f(x)的最大值及最小值,可得實驗室這一天的最大溫差.(Ⅱ)由題意可得,當f(t)>11時,需要降溫,由f(t)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,解得t的范圍,可得結論.
,解得t的范圍,可得結論.


科目:高中數學 來源: 題型:
【題目】已知下列三個命題:
①若一個球的半徑縮小到原來的 ![]() ,則其體積縮小到原來的
,則其體積縮小到原來的![]() ;
;
②若兩組數據的平均數相等,則它們的標準差也相等;
③直線x+y+1=0與圓x2+y2= ![]() 相切.
相切.
其中真命題的序號是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名髙一新生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A、B兩種不同的教學方式分別在甲、乙兩個班級進行教改實驗.為了解教學效果,期末考試后,陳老師對甲、乙兩個班級的學生成績進行統計分析,畫出頻率分布直方圖(如下圖).記成績不低于90分者為“成績優秀”

| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(I)從乙班隨機抽取2名學生的成績,記“成績優秀”的個數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(II)根據頻率分布直方圖填寫下面2 x2列聯表,并判斷是否有95%的把握認為:“成績優秀”與教學方式有關.
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知常數![]() ,在矩形ABCD中,
,在矩形ABCD中, ![]() ,
, ![]() ,O為AB的中點,點E、F、G分別在BC、CD、DA上移動,且
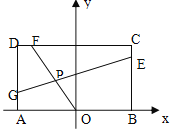
,O為AB的中點,點E、F、G分別在BC、CD、DA上移動,且![]() ,P為GE與OF的交點(如圖),問是否存在兩個定點,使P到這兩點的距離的和為定值?若存在,求出這兩點的坐標及此定值;若不存在,請說明理由
,P為GE與OF的交點(如圖),問是否存在兩個定點,使P到這兩點的距離的和為定值?若存在,求出這兩點的坐標及此定值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設過原點 O 的直線與圓 C : ![]() 的一個交點為 P ,點 M 為線段 OP 的中點。
的一個交點為 P ,點 M 為線段 OP 的中點。
(1)求圓 C 的極坐標方程;
(2)求點 M 軌跡的極坐標方程,并說明它是什么曲線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x+a=0上存在兩點關于直線l:mx+y+1=0對稱. (Ⅰ)求m的值;
(Ⅱ)直線l與圓C交于A,B兩點, ![]()
![]() =﹣3(O為坐標原點),求圓C的方程.
=﹣3(O為坐標原點),求圓C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“ALS冰桶挑戰賽”是一項社交網絡上發起的籌款活動,活動規定:被邀請者要么在24小時內接受挑戰,要么選擇為慈善機構捐款(不接受挑戰),并且不能重復參加該活動.若被邀請者接受挑戰,則他需在網絡上發布自己被冰水澆遍全身的視頻內容,然后便可以邀請另外3個人參與這項活動.假設每個人接受挑戰與不接受挑戰是等可能的,且互不影響.
附: ![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(1)若某參與者接受挑戰后,對其他3個人發出邀請,則這3個人中恰有2個人接受挑戰的概率是多少?
(2)為了解冰桶挑戰賽與受邀者的性別是否有關,某調查機構進行了隨機抽樣調查,調查得到如下 ![]() 列聯表:
列聯表:
接受挑戰 | 不接受挑戰 | 合計 | |
男性 | 50 | 10 | 60 |
女性 | 25 | 15 | 40 |
合計 | 75 | 25 | 100 |
根據表中數據,是否有99%的把握認為“冰桶挑戰賽與受邀者的性別有關”?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com