如果正實數a,b滿足ab=ba.且a<1,證明a=b.
證一:由a
b=b
a,得blna=alnb,從而

考慮函數

,它的導數是
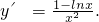
因為在(0,1)內f'(x)>0,所以f(x)在(0,1)內是增函數
由于0<a<1,b>0,所以a
b<1,從而b
a=a
b<1.由b
a<1及a>0,
可推出b<1.
由0<a<1,0<b<1,假如a≠b,
則根據f(x)在(0,1)內是增函數,
得f(a)≠f(b),即
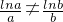
,
從而a
b≠b
a這與a
b=b
a矛盾
所以a=b
證二:因為0<a<1,a
b=b
a,
所以blog
aa=alog
ab,即
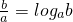
假如a<b,則
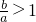
,但因a<1,
根據對數函數的性質,
得
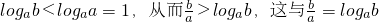
矛盾
所以a不能小于b
假如a>b,則
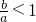
,而log
ab>1,這也與
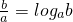
矛盾
所以a不能大于b,因此a=b
證三:假如a<b,則可設b=a+ε,其中ε>0
由于0<a<1,ε>0,
根據冪函數或指數函數的性質,得a
ε<1和
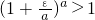
,
所以
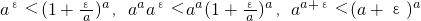
,
即a
b<b
a.這與a
b=b
a矛盾,所以a不能小于b
假如b<a,則b<a<1,可設a=b+ε,其中ε>0,同上可證得a
b<b
a.
這于a
b=b
a矛盾,所以a不能大于b
因此a=b
分析:這道題可以有三種不同的證明方法.證法一的思路:由a
b=b
a,得blna=alnb,從而

,考慮函數

,它的導數是
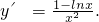
然后根據函數的單調性用反證法進行證明.
證法二的思路是因為0<a<1,a
b=b
a,所以blog
aa=alog
ab,即
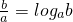
.然后根據對數函數的性質用反證法進行證明.
證法三的思路是假如a<b,則可設b=a+ε,其中ε>0由于0<a<1,ε>0,根據冪函數或指數函數的性質用反證法進行證明.
點評:反證法是證明的一種重要方法,一題多證、舉一反三能夠有效地提高我們的證明能力.


 ,它的導數是
,它的導數是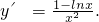
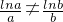 ,
,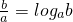
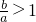 ,但因a<1,
,但因a<1,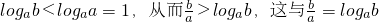 矛盾
矛盾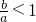 ,而logab>1,這也與
,而logab>1,這也與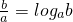 矛盾
矛盾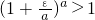 ,
,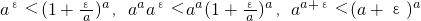 ,
, ,考慮函數
,考慮函數 ,它的導數是
,它的導數是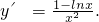 然后根據函數的單調性用反證法進行證明.
然后根據函數的單調性用反證法進行證明.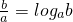 .然后根據對數函數的性質用反證法進行證明.
.然后根據對數函數的性質用反證法進行證明.

 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案