
已知函數![]() 為常數)是實數集
為常數)是實數集![]() 上的奇函數,函數
上的奇函數,函數![]() ,使
,使![]() 在區間
在區間![]() 上是減函數的
上是減函數的![]() 的取值的集合為
的取值的集合為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ) 對![]()
![]() 及
及![]()
![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的最大值;
的最大值;
(Ⅲ)若關于![]() 的方程
的方程![]() 有且只有一個實數根,求
有且只有一個實數根,求![]() 的值.
的值.
解:(Ⅰ)![]() 是實數集
是實數集![]() 上奇函數,
上奇函數,
![]() ,即
,即![]() .
.
將![]() 帶入
帶入![]() ,顯然為奇函數 …………………………………3分
,顯然為奇函數 …………………………………3分
(Ⅱ)由(Ⅰ)知![]() ,
,![]()
![]() 要使
要使![]() 是區間
是區間![]() 上的減函數,則有
上的減函數,則有![]() 在
在![]() 恒成立,
恒成立,![]() ,所以
,所以![]() ………………………………5分
………………………………5分
要使![]() 在
在![]() 上恒成立,
上恒成立,
只需![]() 在
在![]() 時恒成立即可.
時恒成立即可.
![]() (其中
(其中![]() )恒成立即可
)恒成立即可
令![]() ,則
,則![]() 即
即![]()
![]() ,所以實數的最大值為
,所以實數的最大值為![]() ………………………………8分
………………………………8分
(Ⅲ)由(Ⅰ)知方程![]() ,即
,即![]() ,
,
令![]() ,
,![]()
當![]() 時,
時,![]() 在
在![]() 上為增函數;
上為增函數;
當![]() 時,
時,![]() 在
在![]() 上為減函數;
上為減函數;
當![]() 時,
時,![]() ……………………………………………………11分
……………………………………………………11分
而![]()
當![]() 時
時![]() 是減函數,當
是減函數,當![]() 時,
時,![]() 是增函數,
是增函數,
![]() 當
當![]() 時,
時,![]() ……………………………………………13分
……………………………………………13分
只有當![]() ,即
,即![]() 時,方程有且只有一個實數根。 ……………14分
時,方程有且只有一個實數根。 ……………14分


 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
(本小題滿分16分)
已知函數![]() (
(![]() 為實常數).
為實常數).
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若![]() ,設
,設![]() 在區間
在區間![]() 的最小值為
的最小值為![]() ,求
,求![]() 的表達式;
的表達式;
(3)設![]() ,若函數
,若函數![]() 在區間
在區間![]() 上是增函數,求實數
上是增函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分16分)
已知函數![]() (
(![]() 為實常數).
為實常數).
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若![]() ,設
,設![]() 在區間
在區間![]() 的最小值為
的最小值為![]() ,求
,求![]() 的表達式;
的表達式;
(3)設![]() ,若函數
,若函數![]() 在區間
在區間![]() 上是增函數,求實數
上是增函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分16分)
已知函數![]() (
(![]() 為實常數).
為實常數).
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若![]() ,設
,設![]() 在區間
在區間![]() 的最小值為
的最小值為![]() ,求
,求![]() 的表達式;
的表達式;
(3)設![]() ,若函數
,若函數![]() 在區間
在區間![]() 上是增函數,求實數
上是增函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省東莞市五校高三第一次聯考文科數學卷 題型:解答題
已知函數 (
( 為實常數).
為實常數).
(1)當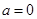 時,求
時,求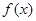 的最小值;
的最小值;
(2)若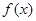 在
在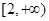 上是單調函數,求
上是單調函數,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011--2012學年山西省第一學期高一月考數學試卷 題型:解答題
已知函數 (
( 為實常數).
為實常數).
(1)若 ,求
,求 的單調區間;
的單調區間;
(2)若 ,設
,設 在區間
在區間 的最小值為
的最小值為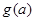 ,求
,求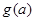 的表達式;
的表達式;
(3)設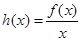 ,若函數
,若函數 在區間
在區間 上是增函數,求實數
上是增函數,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com