
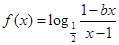 為奇函數,
為奇函數,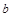 為常數.
為常數.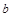 的值;
的值; 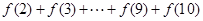 的值;
的值;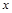 的值,不等式
的值,不等式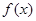 >
>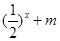 恒成立,求實數
恒成立,求實數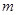 的取值范圍.
的取值范圍.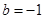 ;
;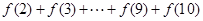 =
=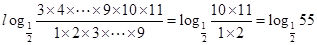 ;
;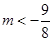 。
。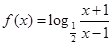 ,得
,得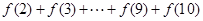 =
=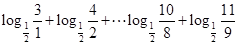 這是求解此步的關鍵,然后再利用對數的運算法則求值即可。
這是求解此步的關鍵,然后再利用對數的運算法則求值即可。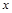 的值,不等式
的值,不等式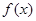 >
>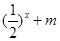 恒成立轉化為當
恒成立轉化為當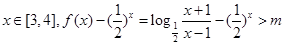 恒成立,然后再構造函數:
恒成立,然后再構造函數: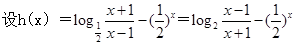 研究出h(x)是增函數,從而可求出h(x)的最小值,問題得解。
研究出h(x)是增函數,從而可求出h(x)的最小值,問題得解。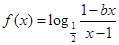 為奇函數
為奇函數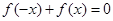 ,即
,即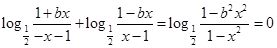 …2分
…2分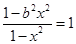 ,解得
,解得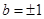 ………………………4分
………………………4分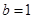 顯然不成立,舍去。所以
顯然不成立,舍去。所以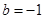 ………………………………………5分
………………………………………5分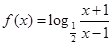
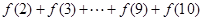 =
=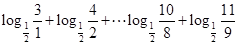 ……6分
……6分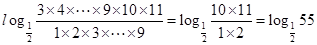 ………………………9分
………………………9分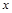 的值,不等式
的值,不等式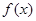 >
>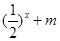 恒成立
恒成立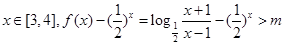 恒成立…………………10分
恒成立…………………10分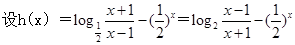 …………………11分
…………………11分 在[3,4]上單調遞增,
在[3,4]上單調遞增,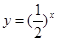 單調遞減
單調遞減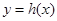 在[3,4]上單調遞增 …………………………………………12分
在[3,4]上單調遞增 …………………………………………12分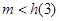 即可
即可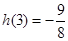 所以
所以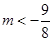 ……………………………………………14分
……………………………………………14分


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com