
在直角坐標系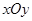 中,
中, 是過定點
是過定點 且傾斜角為
且傾斜角為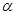 的直線;在極坐標系(以坐標原點
的直線;在極坐標系(以坐標原點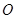 為極點,以
為極點,以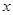 軸非負半軸為極軸,取相同單位長度)中,曲線
軸非負半軸為極軸,取相同單位長度)中,曲線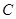 的極坐標方程為
的極坐標方程為 .
.
(I)寫出直線 的參數方程;并將曲線
的參數方程;并將曲線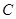 的方程化為直角坐標方程;
的方程化為直角坐標方程;
(II)若曲線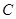 與直線相交于不同的兩點
與直線相交于不同的兩點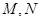 ,求
,求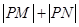 的取值范圍.
的取值范圍.
(I)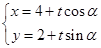 (
(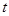 為參數);
為參數); .(II)
.(II)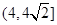 .
.
【解析】
試題分析:(I)根據直線的參數方程公式已知,直線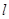 的參數方程為
的參數方程為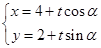 (
(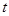 為參數);要轉化曲線
為參數);要轉化曲線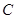 的極坐標方程,只需在等式兩邊同乘
的極坐標方程,只需在等式兩邊同乘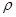 ,得
,得 ,故
,故 ;( II)具體做法可以將直線轉化成直角坐標方程形式或者直接帶入,也可以直接將
;( II)具體做法可以將直線轉化成直角坐標方程形式或者直接帶入,也可以直接將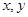 直接帶入,而且都和參數
直接帶入,而且都和參數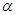 有關,所以可以可以直接將
有關,所以可以可以直接將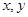 帶入,根據
帶入,根據 判別式,韋達定理找出
判別式,韋達定理找出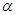 的取值范圍;接著用含
的取值范圍;接著用含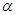 的形式表示出
的形式表示出 ,
,
根據三角函數知識求出 范圍.
范圍.
試題解析:(I)直線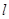 的參數方程為
的參數方程為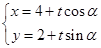 (
(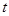 為參數).
為參數).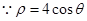 ,
,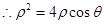 ,所以
,所以 .
.
(II)直線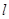 的參數方程為
的參數方程為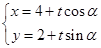 (
(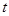 為參數),帶入
為參數),帶入 ,得
,得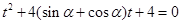 ,則有
,則有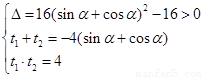 ,
,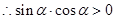 ,又
,又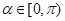 ,所以
,所以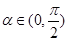 ,
,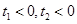 .而
.而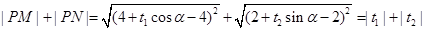
 .
.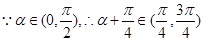 ,
,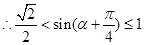 ,
,
所以 的取值范圍為
的取值范圍為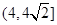 .
.
考點:1.參數方程,極坐標方程與直角坐標方程的轉化;2.三角函數的最值求解.


科目:高中數學 來源: 題型:
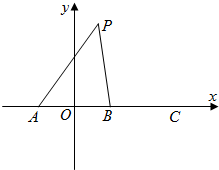 如圖,在直角坐標系中,A,B,C三點在x軸上,原點O和點B分別是線段AB和AC的中點,已知AO=m(m為常數),平面上的點P滿足PA+PB=6m.
如圖,在直角坐標系中,A,B,C三點在x軸上,原點O和點B分別是線段AB和AC的中點,已知AO=m(m為常數),平面上的點P滿足PA+PB=6m.| x |
| 3 |
| y | ||
2
|
查看答案和解析>>
科目:高中數學 來源: 題型:
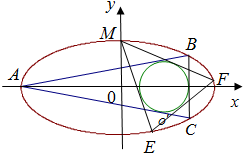 如圖,在直角坐標系中,中心在原點,焦點在X軸上的橢圓G的離心率為e=
如圖,在直角坐標系中,中心在原點,焦點在X軸上的橢圓G的離心率為e=
| ||
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (1)如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線AD交⊙O于D,DE⊥AC交AC延長線于點E,OE交AD于點F.
(1)如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線AD交⊙O于D,DE⊥AC交AC延長線于點E,OE交AD于點F.| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
|
查看答案和解析>>
科目:高中數學 來源:2013-2014學年云南省昆明市高三上學期第一次摸底調研測試文科數學試卷(解析版) 題型:解答題
在直角坐標系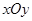 中,
中, 是過定點
是過定點 且傾斜角為
且傾斜角為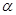 的直線;在極坐標系(以坐標原點
的直線;在極坐標系(以坐標原點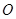 為極點,以
為極點,以 軸非負半軸為極軸,取相同單位長度)中,曲線
軸非負半軸為極軸,取相同單位長度)中,曲線 的極坐標方程為
的極坐標方程為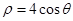 .
.
(I)寫出直線 的參數方程;并將曲線
的參數方程;并將曲線 的方程化為直角坐標方程;
的方程化為直角坐標方程;
(II)若曲線 與直線相交于不同的兩點
與直線相交于不同的兩點 ,求
,求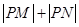 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com