
 個單位后,得到函數y=g(x)的圖象,若
個單位后,得到函數y=g(x)的圖象,若 ,α為第一象限角,求sin2α值.
,α為第一象限角,求sin2α值. )的值,由α為第一象限角,得出2α-
)的值,由α為第一象限角,得出2α- 的范圍,再根據sin(2α-
的范圍,再根據sin(2α- )的范圍,利用同角三角函數間的基本關系求出cos(2α-
)的范圍,利用同角三角函數間的基本關系求出cos(2α- )的值,將所求式子中的角2α變形為(2α-
)的值,將所求式子中的角2α變形為(2α- )+
)+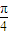 ,利用兩角和與差的正弦函數公式及特殊角的三角函數值化簡后,將各自的值代入即可求出值.
,利用兩角和與差的正弦函數公式及特殊角的三角函數值化簡后,將各自的值代入即可求出值. sin(2x+
sin(2x+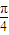 )+1,
)+1, ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ (k∈Z)得:kπ-
(k∈Z)得:kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z, ,kπ+
,kπ+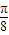 ](k∈Z);
](k∈Z); sin(2x-
sin(2x- )+1,
)+1, sin(2α-
sin(2α- )+1=
)+1= +1,
+1, )=
)= ,
, ∈(4kπ-
∈(4kπ- ,4kπ+
,4kπ+ ),k∈Z,
),k∈Z, )<
)< <
< 知,
知, ∈(4kπ,4kπ+
∈(4kπ,4kπ+ ),k∈Z,
),k∈Z, )=
)= ,
,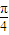 )+
)+ ]=
]= [sin(2α-
[sin(2α- )+cos(2α-
)+cos(2α- )]=
)]= (
( +
+ )=
)= .
.

科目:高中數學 來源: 題型:
| 1 |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com