
【題目】如圖,點P是菱形ABCD所在平面外一點,且![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() .
.
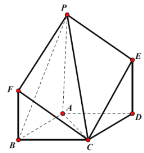
(1)求證:平面![]() 平面PCE;
平面PCE;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)取PC中點M,連接BD交AC于O,連接OM,EM.根據菱形性質可得![]() ,再由
,再由![]() 即可證明
即可證明![]() 平面PAC,進而利用平行四邊形性質可證明
平面PAC,進而利用平行四邊形性質可證明![]() ,即可得
,即可得![]() 平面PAC,結合平面與平面垂直的判定即可證明平面
平面PAC,結合平面與平面垂直的判定即可證明平面![]() 平面
平面![]() ;
;
(2)以OB,OC,OM所在直線分別為x軸,y軸,z軸建立空間直角坐標系,由題意可設![]() ,寫出各個點的坐標.利用向量的數量積求得平面
,寫出各個點的坐標.利用向量的數量積求得平面![]() 和
和
平面![]() 的法向量,即可利用空間向量數量積的運算求得夾角的余弦值.
的法向量,即可利用空間向量數量積的運算求得夾角的余弦值.
(1)證明:取PC中點M,連接BD交AC于O,連接OM,EM.如下圖所示:
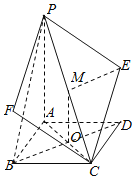
在菱形ABCD中,![]() ,
,
![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() ,
,
又![]() ,PA,
,PA,![]() 平面PAC,
平面PAC,
![]() 平面PAC,
平面PAC,
![]() ,M分別是AC,PC的中點,
,M分別是AC,PC的中點,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四邊形OMED是平行四邊形,則
四邊形OMED是平行四邊形,則![]() ,
,
![]() 平面PAC,
平面PAC,
又![]() 平面PCD,
平面PCD,
![]() 平面
平面![]() 平面PCE.
平面PCE.
(2)由(1)得![]() 平面PAC﹐則OB,OC,OM兩兩垂直,以OB,OC,OM所在直線分別為x軸,y軸,z軸建立空間直角坐標系,如下圖所示
平面PAC﹐則OB,OC,OM兩兩垂直,以OB,OC,OM所在直線分別為x軸,y軸,z軸建立空間直角坐標系,如下圖所示
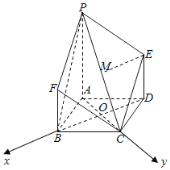
設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
設![]() 是平面BPC的一個法向量,則
是平面BPC的一個法向量,則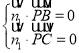 ,即
,即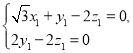 ,
,![]() ,
,
設![]() 是平面FPC的一個法向量,同理得,
是平面FPC的一個法向量,同理得,![]()
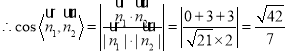 ,
,
由圖可知二面角![]() 為銳二面角
為銳二面角
![]() 二面角
二面角![]() 的余弦值為
的余弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知數組![]() ,如果數組
,如果數組![]() 滿足
滿足![]() ,且
,且![]() ,其中
,其中![]()
![]() ,則稱
,則稱![]() 為
為![]() 的“兄弟數組”.
的“兄弟數組”.
(1)寫出數組![]() 的“兄弟數組”
的“兄弟數組”![]() ;
;
(2)若![]() 的“兄弟數組”是
的“兄弟數組”是![]() ,試證明:
,試證明:![]() 成等差數列;
成等差數列;
(3)若![]() 為偶數,且
為偶數,且![]() 的“兄弟數組”是
的“兄弟數組”是![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的個數為( )
①“ac<0”是“二次函數y=ax2+bx+c(a,b,c∈R)有兩個異號零點”的必要不充分條件;
②”sinθ![]() ”是“θ
”是“θ![]() ”充分不必要條件;
”充分不必要條件;
③“偶函數的圖象關于直線x=0成軸對稱”的逆否命題;
④“若sinx﹣cosx![]() ,則sinx+cosx
,則sinx+cosx![]() 的逆命題;
的逆命題;
⑤設a,b∈R,則“a>b”是“a|a|>b|b|”的充分條件
A.1B.2C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線l的參數方程為
中,直線l的參數方程為![]() (t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]()
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)若直線l與曲線C相交于A,B兩點.求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的單調區間;
(2)設g(x)=lnx![]() ,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
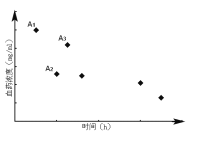
【題目】如圖為服用同等劑量的三種新藥后血藥濃度![]() 的變化情況,其中點
的變化情況,其中點![]() 的橫坐標表示服用第
的橫坐標表示服用第![]() 種藥后血藥濃度達峰(最高濃度)時間,其它點的橫坐標分別表示服用三種新藥后血藥濃度首次降到峰值一半時所用的時間(單位:
種藥后血藥濃度達峰(最高濃度)時間,其它點的橫坐標分別表示服用三種新藥后血藥濃度首次降到峰值一半時所用的時間(單位:![]() ),點
),點![]() 的縱坐標表示第
的縱坐標表示第![]() 種藥的血藥濃度的峰值
種藥的血藥濃度的峰值![]() . 記
. 記![]() 為服用第
為服用第![]() 種藥后達到血藥濃度峰值時,血藥濃度提高的平均速度,記
種藥后達到血藥濃度峰值時,血藥濃度提高的平均速度,記![]() 為服用第
為服用第![]() 種藥后血藥濃度從峰值首次降到峰值的一半所用的時間,則
種藥后血藥濃度從峰值首次降到峰值的一半所用的時間,則![]() 中最小的,
中最小的,![]() 中最大的分別是( )
中最大的分別是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com