日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】三棱錐中, , △是斜邊的等腰直角三角形, 以下結(jié)論中: ① 異面直線與所成的角為；② 直線平面；③ 面面；④ 點(diǎn)到平面的距離是. 其中正確結(jié)論的序號(hào)是 ____________________ .

【答案】①②③④

【解析】由題意三棱錐SABC中,∠SBA=∠SCA=90°，知SB⊥BA，SC⊥CA，

又△ABC是斜邊AB=a的等腰直角三角形可得AC⊥BC，又BC∩SB=B，故有AC⊥面SBC，故有SB⊥AC，故①正確，

由此可以得到SB⊥平面ABC，故②正確，

再有AC面SAC得面SBC⊥面SAC，故③正確，

△ABC是斜邊AB=a的等腰直角三角形,點(diǎn)C到平面SAB的距離即點(diǎn)C到斜邊AB的中點(diǎn)的距離,即 ，故④正確。

故答案為①②③④

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：

【題目】已知向量， ．設(shè) (t為實(shí)數(shù))．

（Ⅰ）若，求當(dāng)取最小值時(shí)實(shí)數(shù)t的值；

（Ⅱ）若⊥，問：是否存在實(shí)數(shù)t，使得向量－和向量的夾角為，若存在，請求出t；若不存在，請說明理由．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】已知函數(shù)（其中為自然對數(shù)的底數(shù)，）．

（1）若僅有一個(gè)極值點(diǎn)，求的取值范圍；

（2）證明：當(dāng)時(shí)，有兩個(gè)零點(diǎn)，且．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】已知全集U=R，A={x|x2﹣2x﹣3≤0}，B={x|2≤x＜5}，C={x|x＞a}．

（1）求A∩（UB）；

（2）若A∪C=C，求a的取值范圍．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】函數(shù)y＝a2x＋2ax－1(a＞0且a≠1)，當(dāng)自變量x∈[－1,1]時(shí)，函數(shù)的最大值為14.試求a的值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】已知拋物線C的一個(gè)焦點(diǎn)為，對應(yīng)于這個(gè)焦點(diǎn)的準(zhǔn)線方程為

（1）寫出拋物線C的方程；

（2）過F點(diǎn)的直線與曲線C交于A、B兩點(diǎn)，O點(diǎn)為坐標(biāo)原點(diǎn)，求△AOB重心G的軌跡方程；

（3）點(diǎn)P是拋物線C上的動(dòng)點(diǎn)，過點(diǎn)P作圓的切線，切點(diǎn)分別是M，N.當(dāng)P點(diǎn)在何處時(shí)，|MN|的值最小？求出|MN|的最小值.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】選修4-4：坐標(biāo)系與參數(shù)方程

在平面直角坐標(biāo)系中，直線的參數(shù)方程是（為參數(shù)），以為極點(diǎn)， 軸的正半軸為極軸，建立極坐標(biāo)系，曲線的極坐標(biāo)方程為，且直線與曲線交于兩點(diǎn).

（Ⅰ）求曲線的直角坐標(biāo)方程及直線恒過的定點(diǎn)的坐標(biāo)；

（Ⅱ）在（Ⅰ）的條件下，若，求直線的普通方程.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】如圖，四邊形為菱形，四邊形為平行四邊形，設(shè)與相交于點(diǎn)，．

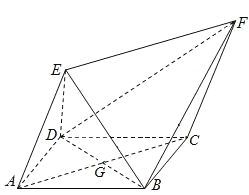
（1）證明：平面平面；

（2）若，求三棱錐的體積．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】通過研究學(xué)生的學(xué)習(xí)行為,專家發(fā)現(xiàn),學(xué)生的注意力著老師講課時(shí)間的變化而變化,講課開始時(shí),學(xué)生的興趣激增;中間有一段時(shí)間,學(xué)生的興趣保持較理想的狀態(tài),隨后學(xué)生的注意力開始分散,設(shè)f(t)表示學(xué)生注意力隨時(shí)間t(分鐘)的變化規(guī)律\left(f(t)越大,表明學(xué)生注意力越集中),經(jīng)過實(shí)驗(yàn)分析得知：

(1)講課開始后多少分鐘，學(xué)生的注意力最集中?能持續(xù)多少分鐘?

(2)講課開始后5分鐘與講課開始后25分鐘比較，何時(shí)學(xué)生的注意力更集中?

(3)一道數(shù)學(xué)難題，需要講解24分鐘，并且要求學(xué)生的注意力至少達(dá)到180，那么經(jīng)過適當(dāng)安排，教師能否在學(xué)生達(dá)到所需的狀態(tài)下講授完這道題目?

查看答案和解析>>

同步練習(xí)冊答案
主站蜘蛛池模板： 一区二区久久 | 国产干干干 | 日韩视频免费在线 | 女人口述交换啪啪高潮过程 | 99精品一区二区 | 爱爱视频天天看 | 国产高清无av久久 | 欧美www. | 极品美女中出 | www.国产在线 | 日本在线视频观看 | 蜜桃视频麻豆女神沈芯语免费观看 | 日韩免费在线观看视频 | 成人免费视频国产免费麻豆 | 国产高清av在线一区二区三区 | 在线播放精品 | 在线国产一区二区 | 爱爱视频免费播放 | 一级片日韩| 一区二区三区欧美在线 | 国产精品欧美久久久久一区二区 | 精品亚洲永久免费精品 | 成人午夜视频在线观看 | 精品国产一区二区三区国产馆杂枝 | 男女视频在线观看 | 在线看片网站 | 91久久综合亚洲鲁鲁五月天 | 久久不卡日韩美女 | 99久久久99久久国产片鸭王 | 81精品国产乱码久久久久久 | 日本精品免费 | 仙人掌旅馆在线观看 | 欧美成人h | 国产精品人人做人人爽人人添 | 狠狠操狠狠摸 | 国产一二三区在线播放 | 成人一区二区三区 | 日日撸| 欧美精品网站 | 亚洲国产婷婷香蕉久久久久久 | 久久91久久久久麻豆精品 |