
已知各項均不為零的數列{an}的前n項和為Sn,且滿足a1=c,2Sn=anan+1+r.
(1)若r=-6,數列{an}能否成為等差數列?若能,求![]() 滿足的條件;若不能,請說明理由.
滿足的條件;若不能,請說明理由.
(2)設![]() ,
,![]() ,
,
若r>c>4,求證:對于一切n∈N*,不等式![]() 恒成立.
恒成立.
解:(1)n=1時,2a1=a1a2+r,∵a1=c≠0,∴2c=ca2+r,![]() . (1分)
. (1分)
n≥2時,2Sn=anan+1+r,① 2Sn-1=an-1an+r,②
①-②,得2an=an(an+1-an-1).∵an≠0,∴an+1-an-1=2. ( 3分)
則a1,a3,a5,…,a2n-1,… 成公差為2的等差數列,a2n-1=a1+2(n-1).
a2,a4,a6,…,a2n,… 成公差為2的等差數列, a2n=a2+2(n-1).
要使{an}為等差數列,當且僅當a2-a1=1.即![]() .r=c-c2. ( 4分)
.r=c-c2. ( 4分)
∵r=-6,∴c2-c-6=0,c=-2或3.
∵當c=-2,![]() ,不合題意,舍去.
,不合題意,舍去.
∴當且僅當![]() 時,數列
時,數列![]() 為等差數列 (5分)
為等差數列 (5分)
(2)![]() =[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=
=[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=![]() -2.
-2.
![]() =[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(
=[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(![]() ). (8分)
). (8分)
∴![]()
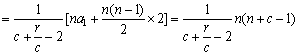 (9分)
(9分)
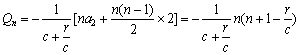 . (10分)
. (10分)
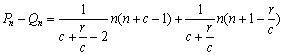 =
=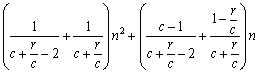 .(11分)
.(11分)
∵r>c>4,∴![]() >4,∴
>4,∴![]() >2.∴0<
>2.∴0<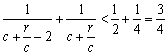 <1. (13分)
<1. (13分)
且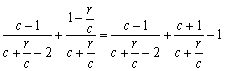 >-1. (14分)
>-1. (14分)
又∵r>c>4,∴![]() ,則0<
,則0<![]() .
.![]() .
.
∴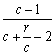 <1.
<1.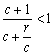 .∴
.∴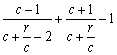 <1.(15分)
<1.(15分)
∴對于一切n∈N*,不等式![]() 恒成立.(16分)
恒成立.(16分)
附加題部分


科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| a6 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| cn |
| bn |
A、若?n∈N*總有
| ||||
B、若?n∈N*總有
| ||||
C、若?n∈N*總有
| ||||
D、若?n∈N*總有
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 4 |
| 1 |
| an |
| 2 |
| k-1 |
| 3n+4 |
| 3n+5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a1 |
| a1-a2 |
| a1 |
| a1-a2 |
| a3 |
| a3-a4 |
| a2n-1 |
| a2n-1-a2n |
| a2 |
| a2-a3 |
| a4 |
| a4-a5 |
| a2n |
| a2n-a2n+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com