
【題目】已知函數![]() .
.
(1)若曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行,求
軸平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)寫出![]() 所有可能的零點個數及相應的
所有可能的零點個數及相應的![]() 的取值范圍.(請直接寫出結論)
的取值范圍.(請直接寫出結論)
 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】從廣安市某中學校的![]() 名男生中隨機抽取
名男生中隨機抽取![]() 名測量身高,被測學生身高全部介于
名測量身高,被測學生身高全部介于![]() cm和
cm和![]() cm之間,將測量結果按如下方式分成八組:第一組
cm之間,將測量結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,...,第八組
,...,第八組![]() ,如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為
,如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為![]() 人.
人.
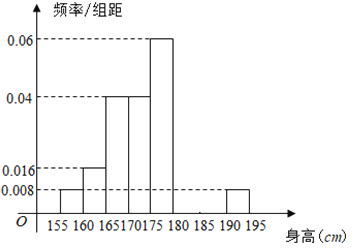
(1)求第七組的頻率;
(2)估計該校![]() 名男生的身高的中位數。
名男生的身高的中位數。
(3)若從樣本中身高屬于第六組和第八組的所有男生中隨機抽取兩名男生,求抽出的兩名男生是同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2ex﹣1(a≠0).
(1)求函數f(x)的單調區間;
(2)已知a>0且x∈[1,+∞),若函數f(x)沒有零點,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在區間[0,1]上的函數y=f(x)的圖象如圖所示.對滿足0<x1<x2<1的任意x1,x2,給出下列結論:
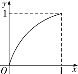
①f(x1)-f(x2)>x1-x2;
②f(x1)-f(x2)<x1-x2;
③x2f(x1)>x1f(x2);
④![]() .
.
其中正確結論的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為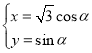 (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() 為曲線
為曲線![]() 上位于第一,二象限的兩個動點,且
上位于第一,二象限的兩個動點,且![]() ,射線
,射線![]() 交曲線
交曲線![]() 分別于
分別于![]() ,求
,求![]() 面積的最小值,并求此時四邊形
面積的最小值,并求此時四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知傾斜角為![]() 的直線經過拋物線
的直線經過拋物線![]() 的焦點
的焦點![]() ,與拋物線
,與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設![]() 為拋物線
為拋物線![]() 上任意一點(異于頂點),過
上任意一點(異于頂點),過![]() 做傾斜角互補的兩條直線
做傾斜角互補的兩條直線![]() 、
、![]() ,交拋物線
,交拋物線![]() 于另兩點
于另兩點![]() 、
、![]() ,記拋物線
,記拋物線![]() 在點
在點![]() 的切線
的切線![]() 的傾斜角為
的傾斜角為![]() ,直線
,直線![]() 的傾斜角為
的傾斜角為![]() ,求證:
,求證:![]() 與
與![]() 互補.
互補.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:
滿足:![]() ,且對任意
,且對任意![]() ,
,![]() (s,k,l,
(s,k,l,![]() )都有
)都有![]() ,則稱數列
,則稱數列![]() 為“T”數列.
為“T”數列.
(1)證明:正項無窮等差數列![]() 是“T”數列;
是“T”數列;
(2)記正項等比數列![]() 的前n項之和為
的前n項之和為![]() ,若數列
,若數列![]() 是“T”數列,求數列
是“T”數列,求數列![]() 公比的取值范圍;
公比的取值范圍;
(3)若數列![]() 是“T”數列,且數列
是“T”數列,且數列![]() 的前n項之和
的前n項之和![]() 滿足
滿足![]() ,求證:數列
,求證:數列![]() 是等差數列.
是等差數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com