91视频久久,亚洲精品久久久久久下一站 ,国产二区在线播放

【題目】有甲、乙兩種商品，經(jīng)銷這兩種商品所能獲得的利潤分別是萬元和萬元，它們與投入資金萬元的關(guān)系為：，今有3萬元資金投入經(jīng)營這兩種商品.問：對乙種商品的資金為多少萬元時，能獲得最大利潤？最大利潤為多少？

【答案】對乙種商品投入資金萬元時，利潤最大，最大利潤為萬元.

【解析】

試題分析：設(shè)對乙種商品投入的資金為萬元，則甲種商品投入的資金為萬元，設(shè)獲得的利潤為萬元，則，設(shè)，則，于是函數(shù)轉(zhuǎn)化為，配方得，根據(jù)二次函數(shù)圖象及性質(zhì)可知，當(dāng)時，即時，函數(shù)取得最大值為，因此對乙種商品投入資金為萬元，對甲種資金投入萬元時，利潤最大，最大利潤為萬元.

試題解析：設(shè)對乙種商品投入資金為萬元，則對甲種投入資金為萬元，此時獲得利潤為萬元，則由題意知：

令，則，（）

當(dāng)時，，即，時，

答：對甲資金投入萬元，對乙資金投入萬元時，獲得最大利潤萬元

練習(xí)冊系列答案

歡樂寒假福建教育出版社系列答案

智多星寒假生活新疆美術(shù)攝影出版社系列答案

快樂假期高考狀元假期學(xué)習(xí)方案寒假系列答案

創(chuàng)新學(xué)習(xí)寒假作業(yè)東北師范大學(xué)出版社系列答案

寒假零距離系列答案

高效中考安徽師范大學(xué)出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費(fèi)課程推薦！	初一	初一免費(fèi)課程推薦！
高二	高二免費(fèi)課程推薦！	初二	初二免費(fèi)課程推薦！
高三	高三免費(fèi)課程推薦！	初三	初三免費(fèi)課程推薦！
更多初中、高中輔導(dǎo)課程推薦,點(diǎn)擊進(jìn)入>>

相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：

【題目】已知,函數(shù)，.

（1）指出的單調(diào)性(不要求證明)；

（2）若有求的值；

（3）若，求使不等式恒成立的的取值范圍.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】已知橢圓的離心率為，以橢圓的四個頂點(diǎn)為頂點(diǎn)的四邊形的面積為．

（1）求橢圓的方程；

（2）斜率為的直線過橢圓的右焦點(diǎn)，且與橢圓交與兩點(diǎn)，過線段的中點(diǎn)與垂直的直線交直線于點(diǎn)，若為等邊三角形，求直線的方程．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

【題目】如圖，四邊形是平行四邊形，平面，，，，，，，為的中點(diǎn).

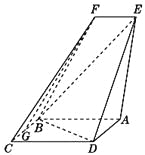
（1）求證：平面；

（2）求證：平面平面；

（3）求多面體的體積.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

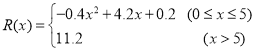【題目】甲廠根據(jù)以往的生產(chǎn)銷售經(jīng)驗(yàn)得到下面有關(guān)生產(chǎn)銷售的統(tǒng)計(jì)規(guī)律：每生產(chǎn)產(chǎn)品（百臺），其總成本為（萬元），其中固定成本為2萬元，并且每生產(chǎn)1百臺的生產(chǎn)成本為1萬元（總成本固定成本+生產(chǎn)成本），銷售收入，假定該產(chǎn)品產(chǎn)銷平衡（即生產(chǎn)的產(chǎn)品都能賣掉），根據(jù)上述統(tǒng)計(jì)規(guī)律，請完成下列問題