
【題目】設函數f (x)=lnx-x+1.
(1)求f (x)的極值;
(2)若0<a<1,證明:函數g (x)=(x-a)ex-![]() ax2+a(a-1) x(x>lna)有極小值點x0,且g (x0)<0.
ax2+a(a-1) x(x>lna)有極小值點x0,且g (x0)<0.
【答案】(1)見解析;(2)見解析
【解析】
(1)求導數![]() ,解方程
,解方程![]() 列表檢查
列表檢查![]() 在
在![]() 的根
的根![]() 左右兩側值的符號,如果左正右負,那么
左右兩側值的符號,如果左正右負,那么![]() 在
在![]() 處取極大值,如果左負右正,那么
處取極大值,如果左負右正,那么![]() 在
在![]() 處取極小值;(2)令
處取極小值;(2)令![]() 得
得![]() ,
,![]() ,由(1)知
,由(1)知![]() ,可得
,可得![]() 有極小值點
有極小值點![]() ,只需證明
,只需證明![]()
![]()
![]() 即可.
即可.
(1)f′(x)的定義域為(0,+∞),f′(x)=![]() ,令f′(x)=0得x=1.
,令f′(x)=0得x=1.
當x變化時,f ′(x),f (x)的變化情況如下表:
x | (0,1) | 1 | (0,+∞) |
f ′(x) | + | 0 | - |
f (x) | ↗ | 極大 | ↘ |
所以當x=1時,f (x)取極大值f (1)=0,沒有極小值.
(2)g′(x)=(ex-a)[ x-(a-1)],令g′(x)=0得x1=lna,x2=a-1.
因為0<a<1,由(1)知lna<a-1.
當x∈(lna,a-1)時,g′(x)<0;當x∈(a-1,+∞)時,g′(x)>0;所以g (x)有極小值點x0=a-1.
由lna<a-1,得ea-1>a.
g (x0)=g (a-1)=![]() a(a-1)2-ea-1<
a(a-1)2-ea-1<![]() a(a-1)2-a=
a(a-1)2-a=![]() a(a2-2a-1).
a(a2-2a-1).
因為0<a<1,所以a2-2a-1<0,因此g (x0)<0.


科目:高中數學 來源: 題型:
【題目】經調查,3個成年人中就有一個高血壓,那么什么是高血壓?血壓多少是正常的?經國際衛生組織對大量不同年齡的人群進行血壓調查,得出隨年齡變化,收縮壓的正常值變化情況如下表:
年齡x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收縮壓 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: ,
,![]() ,
,![]()

![]() 請畫出上表數據的散點圖;
請畫出上表數據的散點圖;
![]() 請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程
請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;![]() 的值精確到
的值精確到![]()
![]() 若規定,一個人的收縮壓為標準值的
若規定,一個人的收縮壓為標準值的![]() 倍,則為血壓正常人群;收縮壓為標準值的
倍,則為血壓正常人群;收縮壓為標準值的![]() 倍,則為輕度高血壓人群;收縮壓為標準值的
倍,則為輕度高血壓人群;收縮壓為標準值的![]() 倍,則為中度高血壓人群;收縮壓為標準值的
倍,則為中度高血壓人群;收縮壓為標準值的![]() 倍及以上,則為高度高血壓人群
倍及以上,則為高度高血壓人群![]() 一位收縮壓為180mmHg的70歲的老人,屬于哪類人群?
一位收縮壓為180mmHg的70歲的老人,屬于哪類人群?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “f(0)![]() ”是“函數f(x)是奇函數”的充要條件
”是“函數f(x)是奇函數”的充要條件
B. 若p:![]() ,
,![]() ,則
,則![]() :
:![]() ,
,![]()
C. “若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
D. 若![]() 為假命題,則p,q均為假命題
為假命題,則p,q均為假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,過右焦點
,過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且當點
兩點,且當點![]() 是橢圓
是橢圓![]() 的上頂點時,
的上頂點時,![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)延長線段![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,若
,若![]() ,求此時
,求此時![]() 的方程.
的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次投籃測試中,有兩種投籃方案:方案甲:先在A點投籃一次,以后都在B點投籃;方案乙:始終在B點投籃.每次投籃之間相互獨立.某選手在A點命中的概率為![]() ,命中一次記3分,沒有命中得0分;在B點命中的概率為
,命中一次記3分,沒有命中得0分;在B點命中的概率為![]() ,命中一次記2分,沒有命中得0分,用隨機變量
,命中一次記2分,沒有命中得0分,用隨機變量![]() 表示該選手一次投籃測試的累計得分,如果
表示該選手一次投籃測試的累計得分,如果![]() 的值不低于3分,則認為其通過測試并停止投籃,否則繼續投籃,但一次測試最多投籃3次.
的值不低于3分,則認為其通過測試并停止投籃,否則繼續投籃,但一次測試最多投籃3次.
(1)若該選手選擇方案甲,求測試結束后所得分![]() 的分布列和數學期望.
的分布列和數學期望.
(2)試問該選手選擇哪種方案通過測試的可能性較大?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知a,b,N都是正數,a≠1,b≠1,證明對數換底公式:logaN=![]() ;
;
(2)寫出對數換底公式的一個性質(不用證明),并舉例應用這個性質.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,錯誤的是( )
A. 在![]() 中,
中, ![]() 則
則![]()
B. 在銳角![]() 中,不等式
中,不等式![]() 恒成立
恒成立
C. 在![]() 中,若
中,若![]() ,則
,則![]() 必是等腰直角三角形
必是等腰直角三角形
D. 在![]() 中,若
中,若![]() ,
, ![]() ,則
,則![]() 必是等邊三角形
必是等邊三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點![]() 的圓
的圓![]() 的圓心
的圓心![]() 在
在![]() 軸的非負半軸上,且圓
軸的非負半軸上,且圓![]() 截直線
截直線![]() 所得弦長為
所得弦長為![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)若過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交圓
交圓![]() 于
于![]() 、
、![]() 兩點,若
兩點,若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解我市參加2018年全國高中數學聯賽的學生考試結果情況,從中選取60名同學將其成績(百分制,均為正數)分成![]() 六組后,得到部分頻率分布直方圖(如圖),觀察圖形,回答下列問題:
六組后,得到部分頻率分布直方圖(如圖),觀察圖形,回答下列問題:
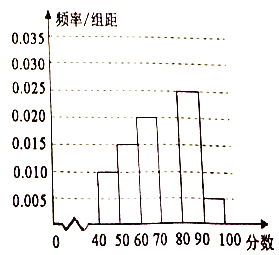
(1)求分數在![]() 內的頻率,并補全這個頻率分布直方圖;
內的頻率,并補全這個頻率分布直方圖;
(2)根據頻率分布直方圖,估計本次考試成績的眾數、均值;
(3)根據評獎規則,排名靠前10%的同學可以獲獎,請你估計獲獎的同學至少需要所少分?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com