
已知函數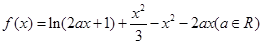
(1)若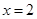 為
為 的極值點,求實數
的極值點,求實數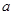 的值;
的值;
(2)若 在
在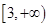 上為增函數,求實數
上為增函數,求實數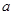 的取值范圍;
的取值范圍;
(3)當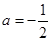 時,方程
時,方程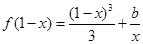 有實根,求實數
有實根,求實數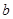 的最大值.
的最大值.
(1) ;(2)
;(2) ;(3)0.
;(3)0.
解析試題分析:(1)先求導數,因為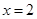 為
為 的極值點,所以
的極值點,所以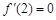 ,所以得出
,所以得出 ;(2)因為
;(2)因為 在區(qū)間
在區(qū)間 上為增函數,所以
上為增函數,所以 恒成立,通過對
恒成立,通過對 和
和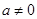 進行討論;(3)將
進行討論;(3)將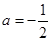 代入方程,得到
代入方程,得到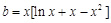 ,所以本題轉化成
,所以本題轉化成 與
與 的交點問題,所以通過求導判斷函數的單調性,畫出函數
的交點問題,所以通過求導判斷函數的單調性,畫出函數 的圖像,得到
的圖像,得到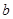 的取值范圍.
的取值范圍.
試題解析:(1)解: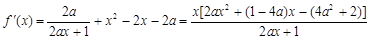 1分
1分
因為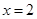 為
為 的極值點,所以
的極值點,所以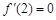 2分
2分
即 ,解得:
,解得: 3分
3分
又當 時,
時, ,從而
,從而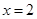 為
為 的極值點成立. 4分
的極值點成立. 4分
(2)解:∵ 在區(qū)間
在區(qū)間 上為增函數,
上為增函數,
∴ 在區(qū)間
在區(qū)間 上恒成立. 5分
上恒成立. 5分
①當 時,
時, 在
在 上恒成立,所以
上恒成立,所以 在
在 上為增函數,
上為增函數,
故 符合題意. 6分
符合題意. 6分
②當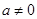 時,由函數
時,由函數 的定義域可知,必須有
的定義域可知,必須有 對
對 恒成立,故只能
恒成立,故只能 ,
,
所以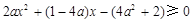 在區(qū)間
在區(qū)間 上恒成立. 7分
上恒成立. 7分
令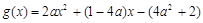 ,其對稱軸為
,其對稱軸為 8分
8分
∵ ,∴
,∴ ,從而
,從而 在
在 上恒成立,只要
上恒成立,只要 即可,
即可,
由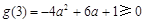 ,解得:
,解得: 9分
9分
∵ ,∴
,∴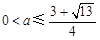 .綜上所述,
.綜上所述,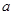 的取值范圍為
的取值范圍為 10分
10分
(3)解: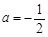 時,方程
時,方程 可化為,
可化為, .
.
問題轉化為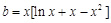 在
在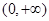 上有解 11分
上有解 11分
令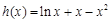 ,則
,則 ks5u 12分
ks5u 12分
當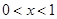 時,
時, ,∴
,∴ 在
在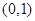 上為增函數
上為增函數
當 時,
時,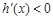 ,∴
,∴ 在
在


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:解答題
如圖,某自來水公司要在公路兩側排水管,公路為東西方向,在路北側沿直線 排,在路南側沿直線
排,在路南側沿直線 排,現(xiàn)要在矩形區(qū)域
排,現(xiàn)要在矩形區(qū)域 內沿直線將
內沿直線將 與
與 接通.已知
接通.已知 ,
, ,公路兩側排管費用為每米1萬元,穿過公路的
,公路兩側排管費用為每米1萬元,穿過公路的 部分的排管費用為每米2萬元,設
部分的排管費用為每米2萬元,設 與
與 所成的小于
所成的小于 的角為
的角為 .
.
(Ⅰ)求矩形區(qū)域 內的排管費用
內的排管費用 關于
關于 的函數關系式;
的函數關系式;
(Ⅱ)求排管的最小費用及相應的角 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=aex,g(x)=lnx-lna,其中a為常數,e=2.718…,且函數y=f(x)和y=g(x)的圖像在它們與坐標軸交點處的切線互相平行.
(1)求常數a的值;(2)若存在x使不等式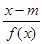 >
> 成立,求實數m的取值范圍;
成立,求實數m的取值范圍;
(3)對于函數y=f(x)和y=g(x)公共定義域內的任意實數x0,我們把|f(x0)-g(x0)|的值稱為兩函數在x0處的偏差.求證:函數y=f(x)和y=g(x)在其公共定義域內的所有偏差都大于2.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)= x
x -ax+(a-1)
-ax+(a-1) ,
, .
.
(1)討論函數 的單調性;(2)若
的單調性;(2)若 ,設
,設 ,
,
(ⅰ)求證g(x)為單調遞增函數;
(ⅱ)求證對任意x ,x
,x

 ,x
,x
 x
x ,有
,有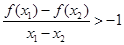 .
.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com