甲、乙、丙三人進行乒乓球練習賽，其中兩人比賽，另一人當裁判，每局比賽結束時，負的一方在下一局當裁判．設各局中雙方獲勝的概率均為
，各局比賽的結果相互獨立，第1局甲當裁判．
（1）求第4局甲當裁判的概率；
（2）用X表示前4局中乙當裁判的次數，求X的分布列和數學期望．
（1）
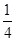（2）
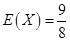
解析試題分析：（1）根據題意，甲第一局當裁判，則第二局一定是參加比賽，第四局當裁判，說明第三局繼續參加比賽，所以，甲參加了第二、三兩局的比賽，且第二局勝，第三局負.
科目：高中數學
來源：
題型：解答題
袋子中放有大小和形狀相同的小球若干，其中標號為0的小球1個，標號為1的小球1個，標號為2的小球n個，已知從袋子中隨機抽取1個小球，取到標號為2的小球的概率是
科目：高中數學
來源：
題型：解答題
某校為組建校籃球隊，對報名同學進行定點投籃測試，規定每位同學最多投3次，每次在A或B處投籃，在A處投進一球得3分，在B處投進一球得2分，否則得0分，每次投籃結果相互獨立，將得分逐次累加并用X表示，如果X的值不低于3分就認為通過測試，立即停止投籃，否則繼續投籃，直到投完三次為止．投籃方案有以下兩種：
科目：高中數學
來源：
題型：解答題
為了參加2013年市級高中籃球比賽，該市的某區決定從四所高中學校選出
科目：高中數學
來源：
題型：解答題
小波以游戲方式決定：是去打球、唱歌還是去下棋.游戲規則為：以O為起點,再從A1,A2,A3,A4,A5,A6(如圖)這6個點中任取兩點分別為終點得到兩個向量，記這兩個向量的數量積為X,若
科目：高中數學
來源：
題型：解答題
袋內裝有6個球，這些球依次被編號為1、2、3、……、6，設編號為n的球重n2－6n＋12(單位：克)，這些球等可能地從袋里取出(不受重量、編號的影響)．
科目：高中數學
來源：
題型：解答題
學校游園活動有這樣一個游戲項目：甲箱子里裝有3個白球，2個黑球，乙箱子里裝有1個白球，2個黑球，這些球除顏色外完全相同．每次游戲從這兩個箱子里各隨機摸出2個球，若摸出的白球不少于2個，則獲獎(每次游戲結束后將球放回原箱)．
科目：高中數學
來源：
題型：解答題
以下莖葉圖記錄了甲、乙兩組各四名同學的植樹棵數．乙組記錄中有一個數據模糊，無法確認，在圖中以X表示．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
（2）根據題意，在四局比賽中，乙參賽的情況與比賽結果可用下表表示五種情況： 第一局 第二局 第三局 第四局 當裁判次數 1 參賽（勝） 參賽（勝） 參賽（勝） 參賽 0 2 參賽（勝） 參賽（勝） 參賽（負） 裁判 1 3 參賽（勝） 參賽（負） 裁判 參賽 1 4 參賽（負） 裁判 參賽（勝） 參賽 1 5 
練習冊系列答案
開拓者系列叢書高中新課標假期作業暑假作業內蒙古人民出版社系列答案
金牛系列高中新課標假期作業暑大眾文藝出版社系列答案
石室金匱暑假作業電子科技大學出版社系列答案
學與練暑假生活寧夏人民教育出版社系列答案
優等生暑假作業云南人民出版社系列答案
志誠教育假期園地暑假作業中原農民出版社系列答案
快樂練習暑假銜接優計劃晨光出版社系列答案
魯人泰斗假期好時光暑假訓練營武漢大學出版社系列答案
培優教材學年總復習給力100長江出版社系列答案
相關習題
.
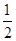(1)求n的值；
(2)從袋子中不放回地隨機抽取2個球，記第一次取出小球標號為a，第二次取出的小球標號為b.①記“a＋b＝2”為事件A，求事件A的概率；
②在區間[0,2]內任取2個實數x，y，求事件“x2＋y2>(a－b)2恒成立”的概率．
方案1：先在A處投一球，以后都在B處投；
方案2：都在B處投籃．
已知甲同學在A處投籃的命中率為0.4，在B處投籃的命中率為0.6.
(1)甲同學若選擇方案1，求X＝2時的概率；
(2)甲同學若選擇方案2，求X的分布列和數學期望；
(3)甲同學選擇哪種方案通過測試的可能性更大？請說明理由．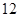
人組成男子籃球隊代表所在區參賽，隊員來源人數如下表：
該區籃球隊經過奮力拼搏獲得冠軍,現要從中選出兩名隊員代表冠軍隊發言．學校
學校甲
學校乙
學校丙
學校丁
人數
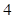
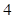
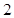
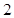
（Ⅰ）求這兩名隊員來自同一學校的概率；
（Ⅱ）設選出的兩名隊員中來自學校甲的人數為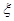
，求隨機變量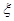的分布列及數學期望
．
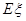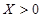就去打球；若
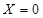就去唱歌；若
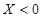就去下棋.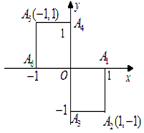
（Ⅰ）分別求小波去下棋的概率和不去唱歌的概率.
（Ⅱ）寫出數量積X的所有可能取值，并求X分布列與數學期望
(1)從袋中任意取出一個球，求其重量大于其編號的概率；
(2)如果不放回地任意取出2個球，求它們重量相等的概率．
(1)求在1次游戲中：
①摸出3個白球的概率；②獲獎的概率．
(2)求在兩次游戲中獲獎次數X的分布列及數學期望E(X)．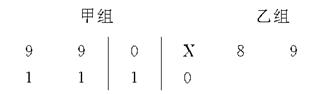
(1)如果X＝8，求乙組同學植樹棵數的平均數和方差；
(2)如果X＝9，分別從甲、乙兩組中隨機選取一名同學，求這兩名同學的植樹總棵數Y的分布列和數學期望．(注：方差s2＝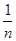
[(x1－
)2＋(x2－)2＋…＋(xn－)2]，其中為x1，x2，…，xn的平均數)
同步練習冊答案
主站蜘蛛池模板：
亚洲激情网站
|
久草精品在线
|
黄色在线免费观看
|
日韩中文字幕视频在线观看
|
亚洲一区电影
|
国产亚洲欧美一区二区
|
日韩成人在线免费观看
|
91九色视频在线
|
91污视频网站
|
日日躁夜夜操
|
久久人人爽人人爽人人片av不
|
亚洲一区二区三区四区五区午夜
|
日韩不卡中文字幕
|
91免费在线
|
天天操天天干天天干
|
国产激情
|
国产精品久久久久久久久久免费
|
成人国产精品久久久
|
成人国产精品一区二区毛片在线
|
成人免费视频一区二区三区
|
免费成人高清
|
男女靠逼视频
|
九九免费视频
|
欧美电影一区二区三区
|
国产精品久久久久一区二区三区
|
午夜精品久久久久久久男人的天堂
|
香蕉二区
|
亚洲精品一区二区网址
|
免费av一区二区三区
|
国产一区二区不卡视频
|
国产乱码精品一区二区三区五月婷
|
国产痴汉av久久精品
|
奇米色777欧美一区二区
|
少妇一区二区三区免费观看
|
成人一区二区av
|
国产一区国产二区在线观看
|
亚洲美女在线视频
|
久久久国产一区二区三区
|
91精品国产乱码久久久久久
|
久久国产精品无码网站
|
久久久久久国产精品
|
版權聲明：本站所有文章，圖片來源于網絡，著作權及版權歸原作者所有，轉載無意侵犯版權，如有侵權，請作者速來函告知，我們將盡快處理，聯系qq：3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號
