
在平面 內,不等式
內,不等式 確定的平面區域為
確定的平面區域為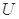 ,不等式組
,不等式組 確定的平面區域為
確定的平面區域為 .
.
(1)定義橫、縱坐標為整數的點為“整點”.在區域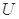 任取3個整點,求這些整點中恰有2個整點在區域
任取3個整點,求這些整點中恰有2個整點在區域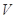 的概率;
的概率;
(2)在區域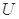 每次任取
每次任取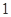 個點,連續取
個點,連續取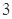 次,得到
次,得到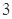 個點,記這
個點,記這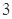 個點在區域
個點在區域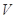 的個數為
的個數為 ,求
,求 的分布列和數學期望.
的分布列和數學期望.
(1)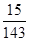
(2) 的分布列為
的分布列為

0 1 2 3 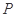
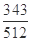
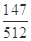
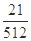
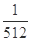
 的數學期望為
的數學期望為 .
.
解析試題分析:(1)作出平面區域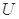 和平面區域
和平面區域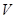 ,打出網格,找出整點,數出在區域
,打出網格,找出整點,數出在區域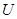 中整點的個數及這些點落在區域
中整點的個數及這些點落在區域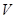 中的個數,運用排列組合知識和古典概型公式求出所求事件的概率;(2)由獨立重復試驗的概念知,每次在區域
中的個數,運用排列組合知識和古典概型公式求出所求事件的概率;(2)由獨立重復試驗的概念知,每次在區域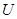 中取一點該點落在區域
中取一點該點落在區域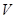 內的概率為定值,取3次,的3個點,落在區域
內的概率為定值,取3次,的3個點,落在區域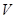 內點的個數服從二項分布,根據二項分布的概率公式和期望公式即可求出分布列與期望.
內點的個數服從二項分布,根據二項分布的概率公式和期望公式即可求出分布列與期望.
試題解析:(1)依題可知平面區域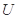 的整點為:
的整點為: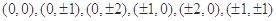 共有13個,上述整點在平面區域
共有13個,上述整點在平面區域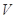 的為:
的為: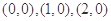 共有3個,
共有3個,
∴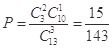 . (4分)
. (4分)
(2)依題可得,平面區域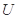 的面積為
的面積為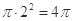 ,
,
平面區域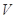 與平面區域
與平面區域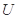 相交部分的面積為
相交部分的面積為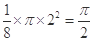 .
.
(設扇形區域中心角為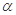 ,則
,則 得
得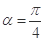 ,也可用向量的夾角公式求
,也可用向量的夾角公式求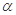 ).
).
在區域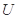 任取1個點,則該點在區域
任取1個點,則該點在區域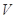 的概率為
的概率為 ,隨機變量
,隨機變量 的可能取值為:
的可能取值為: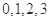 .
. ,
,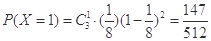 ,
, ,
,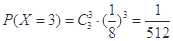 ,
,
∴ 的分布列為
的分布列為

0 1 2 3 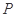
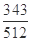
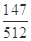
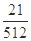
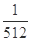
∴ 的數學期望:
的數學期望: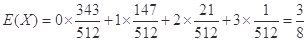 . (12分)
. (12分)
(或者: ~
~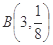 ,故
,故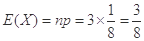 ).
).
考點:二元一次不等式組表示的平面區域,古典概型,二項分布


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
甲乙兩班進行消防安全知識競賽,每班出3人組成甲乙兩支代表隊,首輪比賽每人一道必答題,答對則為本隊得1分,答錯不答都得0分,已知甲隊3人每人答對的概率分別為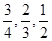 ,乙隊每人答對的概率都是
,乙隊每人答對的概率都是 .設每人回答正確與否相互之間沒有影響,用
.設每人回答正確與否相互之間沒有影響,用 表示甲隊總得分.
表示甲隊總得分.
(I)求隨機變量 的分布列及其數學期望E
的分布列及其數學期望E ;
;
(Ⅱ)求在甲隊和乙隊得分之和為4的條件下,甲隊比乙隊得分高的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
吸煙的危害很多,吸煙產生的煙霧中有近2000種有害物質,如尼古丁、氰氫酸、氨、一氧化碳、二氧化碳、吡啶、砷、銅、鉛等,還有40多種致癌物,如苯并芘、朕苯胺及煤焦油等。它們隨吸煙者吞咽煙霧時進入體內,對機體產生危害。為了解某市心肺疾病是否與吸煙有關,某醫院隨機對入院的50人進行了問卷調查,得到了如下的列聯表.
| | 患心肺疾病 | 不患心肺疾病 | 合計 |
| 吸煙患者 | 20 | 5 | 25 |
| 不吸煙患者 | 10 | 15 | 25 |
| 合計 | 30 | 20 | 50 |
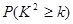 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
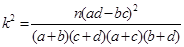 ,其中
,其中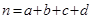
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩人參加某電視臺舉辦的答題闖關游戲,按照規則,甲先從6道備選題中一次任意抽取3道題,獨立作答,然后由乙回答剩余3題,每人答對其中的2題就停止答題,即闖關成功。已知6道備選題中,甲能答對其中的4道題,乙答對每道題的概率都是 .
.
(1)求甲、乙至少有一人闖關成功的概率;
(2)設甲答對題目的個數為 ,求
,求 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校研究性學習小組從汽車市場上隨機抽取20輛純電動汽車調查其續駛里程(單次充電后能行駛的最大里程),被調查汽車的續駛里程全部介于50公里和300公里之間,將統計結果分成5組: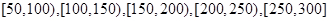 ,繪制成如圖所示的頻率分布直方圖.
,繪制成如圖所示的頻率分布直方圖.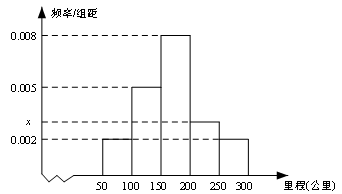
(1)求直方圖中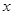 的值;
的值;
(2)求續駛里程在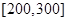 的車輛數;
的車輛數;
(3)若從續駛里程在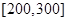 的車輛中隨機抽取2輛車,求其中恰有一輛車的續駛里程為
的車輛中隨機抽取2輛車,求其中恰有一輛車的續駛里程為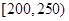 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區為了解高二學生作業量和玩電腦游戲的情況,對該地區內所有高二學生采用隨機抽樣的方法,得到一個容量為200的樣本.統計數據如下:
(1)已知該地區共有高二學生42500名,根據該樣本估計總體,其中喜歡電腦游戲并認為作業不多的人有多少名?
(2)在A,B,C,D,E,F六名學生中,僅有A,B兩名學生認為作業多.如果從這六名學生中隨機抽取兩名,求至少有一名學生認為作業多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
某高校進行自主招生面試時的程序如下:共設3道題,每道題答對給10分、答錯倒扣5分(每道題都必須回答,但相互不影響).設某學生對每道題答對的概率都為 ,則該學生在面試時得分的期望值為 分.
,則該學生在面試時得分的期望值為 分.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
一只不透明的袋子中裝有1個白球和1個紅球,這些球除顏色外其余都相同,攪勻后從中任意摸出1個球,記錄下顏色后放回袋中并攪勻,再從中任意摸出1個球,則 兩次摸出的球顏色相同的概率是 ;
兩次摸出的球顏色相同的概率是 ;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知復數z=x+yi(x,y∈R)在復平面上對應的點為M.
(1)設集合P={-4,-3,-2,0},Q={0,1,2},從集合P中隨機取一個數作為x,從集合Q中隨機取一個數作為y,求復數z為純虛數的概率;
(2)設x∈[0,3],y∈[0,4],求點M落在不等式組: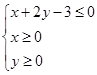 所表示的平面區域內的概率.
所表示的平面區域內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com