
【題目】如圖所示,正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() ,
,![]() ,且
,且![]() ,則下列結論中錯誤的是____________.
,則下列結論中錯誤的是____________.
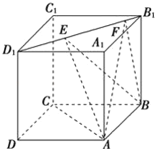
①![]() ;
;
②![]() 平面
平面![]() ;
;
③三棱錐![]() 的體積為定值;
的體積為定值;
④異面直線![]() ,
,![]() 所成的角為定值.
所成的角為定值.
【答案】④
【解析】
①根據正方體的幾何特征,易證![]() 平面
平面![]() . ②根據
. ②根據![]() ,利用線面平行的判定定理判斷.③根據體積公式,判斷
,利用線面平行的判定定理判斷.③根據體積公式,判斷![]() 是否為定值,再根據
是否為定值,再根據![]() 平面
平面![]() ,判斷點A到平面
,判斷點A到平面![]() 的距離是否為定值.④取特殊位置,當E為
的距離是否為定值.④取特殊位置,當E為![]() 的中點,F與
的中點,F與![]() 重合時和當F為
重合時和當F為![]() 的中點,E與
的中點,E與![]() 重合時角是否相等判斷.
重合時角是否相等判斷.
在正方體中,![]() 平面ABCD,所以
平面ABCD,所以![]() AC,又因為
AC,又因為![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,故正確.
,故正確.
②因為![]() 平面
平面![]() ;
;![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故正確.
,故正確.
③因為![]() 是定值,因為
是定值,因為![]() 平面
平面![]() ,點A到平面
,點A到平面![]() 的距離為
的距離為![]() 是定值,故三棱錐
是定值,故三棱錐![]() 的體積為定值,故正確.
的體積為定值,故正確.
④當E為![]() 的中點,F與
的中點,F與![]() 重合時,
重合時,![]() ,
,![]() 異面直線
異面直線![]() ,
,![]() 所成的角
所成的角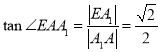 ,當F為
,當F為![]() 的中點,E與
的中點,E與![]() 重合時,
重合時,![]() ,
,![]() 異面直線
異面直線![]() ,
,![]() 所成的角
所成的角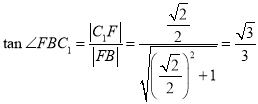 ,所以
,所以![]() ,故異面直線
,故異面直線![]() ,
,![]() 所成的角不是定值,故④錯誤.
所成的角不是定值,故④錯誤.
故答案為:④


科目:高中數學 來源: 題型:
【題目】三棱錐![]() 中,點P是
中,點P是![]() 斜邊AB上一點.給出下列四個命題:
斜邊AB上一點.給出下列四個命題:
①若![]() 平面ABC,則三棱錐
平面ABC,則三棱錐![]() 的四個面都是直角三角形;
的四個面都是直角三角形;
②若S在平面ABC上的射影是斜邊AB的中點P,則有![]() ;
;
③若![]() ,
,![]() ,
,![]() ,
,![]() 平面ABC,則
平面ABC,則![]() 面積的最小值為3;
面積的最小值為3;
④若![]() ,
,![]() ,
,![]() ,
,![]() 平面ABC,則三棱錐
平面ABC,則三棱錐![]() 的外接球體積為
的外接球體積為![]() .
.
其中正確命題的序號是__________.(把你認為正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要排出高三某班一天中,語文、數學、英語各![]() 節,自習課
節,自習課![]() 節的功課表,其中上午
節的功課表,其中上午![]() 節,下午
節,下午![]() 節,若要求
節,若要求![]() 節語文課必須相鄰且
節語文課必須相鄰且![]() 節數學課也必須相鄰(注意:上午第五節和下午第一節不算相鄰),則不同的排法種數是( )
節數學課也必須相鄰(注意:上午第五節和下午第一節不算相鄰),則不同的排法種數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是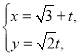 (
(![]() 為參數),曲線
為參數),曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,將曲線
,將曲線![]() 上的點向下平移1個單位,然后橫坐標伸長為原來的2倍,縱坐標不變,得到曲線
上的點向下平移1個單位,然后橫坐標伸長為原來的2倍,縱坐標不變,得到曲線![]() .
.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 和曲線
和曲線![]() 相交于
相交于![]() 兩點,求三角形
兩點,求三角形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定數列![]() ,若滿足
,若滿足![]() (
(![]() 且
且![]() ),對于任意的
),對于任意的![]() ,都有
,都有![]() ,則稱數列
,則稱數列![]() 為“指數型數列”.
為“指數型數列”.
(1)已知數列![]() 的通項公式為
的通項公式為![]() ,試判斷數列
,試判斷數列![]() 是不是“指數型數列”;
是不是“指數型數列”;
(2)已知數列![]() 滿足
滿足![]() ,
,![]() ,證明數列
,證明數列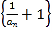 為等比數列,并判斷數列
為等比數列,并判斷數列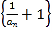 是否為“指數型數列”,若是給出證明,若不是說明理由;
是否為“指數型數列”,若是給出證明,若不是說明理由;
(3)若數列![]() 是“指數型數列”,且
是“指數型數列”,且![]() ,證明數列
,證明數列![]() 中任意三項都不能構成等差數列.
中任意三項都不能構成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的長軸是短軸的兩倍,點
的長軸是短軸的兩倍,點![]() 在橢圓上.不過原點的直線
在橢圓上.不過原點的直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,設直線
兩點,設直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好構成等比數列,
恰好構成等比數列,
(1)求橢圓![]() 的方程;
的方程;
(2)試判斷![]() 是否為定值?若是,求出這個值;若不是,請說明理由?
是否為定值?若是,求出這個值;若不是,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將所有平面向量組成的集合記作![]() ,
,![]() 是從
是從![]() 到
到![]() 的對應關系,記作
的對應關系,記作![]() 或
或![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 都是實數,定義對應關系
都是實數,定義對應關系![]() 的模為:在
的模為:在![]() 的條件下
的條件下![]() 的最大值記作
的最大值記作![]() ,若存在非零向量
,若存在非零向量![]() ,及實數
,及實數![]() 使得
使得![]() ,則稱
,則稱![]() 為
為![]() 的一個特殊值;
的一個特殊值;
(1)若![]() ,求
,求![]() ;
;
(2)如果![]() ,計算
,計算![]() 的特征值,并求相應的
的特征值,并求相應的![]() ;
;
(3)若![]() ,要使
,要使![]() 有唯一的特征值,實數
有唯一的特征值,實數![]() 、
、![]() 、
、![]() 、
、![]() 應滿足什么條件?試找出一個對應關系
應滿足什么條件?試找出一個對應關系![]() ,同時滿足以下兩個條件:①有唯一的特征值
,同時滿足以下兩個條件:①有唯一的特征值![]() ,②
,②![]() ,并驗證
,并驗證![]() 滿足這兩個條件.
滿足這兩個條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形.
)的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形.
(1)求橢圓C的標準方程;
(2)設F為橢圓C的左焦點,T為直線![]() 上任意一點,過F作TF的垂線交橢圓C于點P,Q.
上任意一點,過F作TF的垂線交橢圓C于點P,Q.
(i)證明:OT平分線段PQ(其中O為坐標原點);
(ii)當![]() 最小時,求點T的坐標.
最小時,求點T的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com