Question

已知球O的表面上有P、A、B、C四點,且PA、PB、PC兩兩互相垂直.若PA=PB=PC=a,求這個球的表面積和體積.

Answer 1

解析:設過P、A、B的平面截球所得的截面圓為⊙O₁,PO₁與球面的另一交點為D.

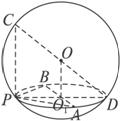
∵PB⊥PA,

∴AB是⊙O₁的直徑且AB=.

∵PC⊥PA,PC⊥PB,

∴PC⊥平面PAB.

又OO₁⊥平面PAB,∴OO₁∥PC.

過OO₁、PC作平面α,則平面α截球面為大圓O.直線DP為平面α和平面PAB的交線，點O₁∈PD,連結CD.在⊙O中,

∵PC⊥PD,∠CPD為直角,

∴CD為⊙O的直徑.

設⊙O的半徑為R,在Rt△CPD中,CD=,即2R=a,

∴R=.∴S_球=4πR²=3πa²,V_球=.

小結：本題先求出PD=AB=a,再利用直角三角形CDP列出a和R之間的關系,并求出R之后求得了表面積和體積.實際上,以PC為棱的正方體的對角線的長等于球的直徑,這是因為,以PC為棱的正方體的外接球就是球O.