日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（本題14分）已知直線：。

（1）求直線關于點對稱的直線的方程；

（2）求直線關于對稱的直線的方程。

解：（1）在直線上取兩點，A、B關于點M(3,2)對稱的點的坐標為，直線的方程為，即所要求的直線方程為。

  （2）由題意知，直線與直線平行，在上取一點P（2，0），P關于的對稱點的坐標為（-3，5），所要求的直線方程為。

練習冊系列答案
相關習題

科目：高中數(shù)學 來源： 題型：

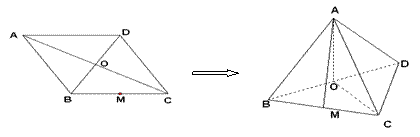
（本題滿分14分）已知菱形的邊長為2，對角線與交于點，且，為的中點.將此菱形沿對角線折成直二面角.

（I）求證：；

（II）求直線與面所成角的余弦值大小.

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

（本題滿分14分）

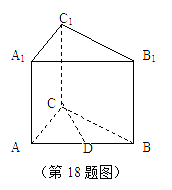已知直三棱柱D是AB的中點．

（1）求證：CD⊥平面ABB1A1；

（2）求二面角D—A1C—A的正切值；

（3）求點C1到平面A1CD的距離．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

（本題滿分14分）

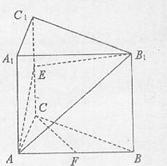
         如圖，已知直三棱柱ABC—A1B1C1，，E是棱CC1上動點，F(xiàn)是AB中點，

   （1）求證：；

   （2）當E是棱CC1中點時，求證：CF//平面AEB1；

   （3）在棱CC1上是否存在點E，使得二面角A—EB1—B的大小是45°，若存在，求CE的長，若不存在，請說明理由。

查看答案和解析>>

科目：高中數(shù)學 來源：2011屆廣東省華南師大附中高三綜合測試數(shù)學理卷 題型：解答題

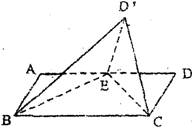
（本題滿分14分） 已知矩形ABCD，AD=2AB=2，點E是AD的中點，將△DEC
沿CE折起到△D’EC的位置，使二面角D'-EC -B是直二面角。
(Ⅰ) 證明：BE⊥CD’；
(Ⅱ) 求二面角D'-BC -E的余弦值，

查看答案和解析>>

科目：高中數(shù)學 來源：2010-2011學年廣東省高三綜合測試數(shù)學理卷 題型：解答題

（本題滿分14分） 已知矩形ABCD，AD=2AB=2，點E是AD的中點，將△DEC

沿CE折起到△D’EC的位置，使二面角D'-EC -B是直二面角。

(Ⅰ) 證明：BE⊥CD’；

(Ⅱ) 求二面角D'-BC -E的余弦值，

 

 

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 欧美一区二区三区免费观看 | 久久福利 | 亚洲精品在线看 | 国产精品视频播放 | 欧美一级特黄aaaaaaa色戒 | 9se成人免费网站 | 成人一区二区三区久久精品嫩草 | 国产精品视频久久久 | 欧美性一区二区 | 羞羞视频网 | 一区二区三区四区免费观看 | 日韩一级片免费在线观看 | 日韩激情二区 | 色就是色欧美 | 欧美一区二区三区四区在线观看 | 国产精品日韩精品 | 国产一区二区三区免费在线 | 亚洲精品三级 | 四虎国产精品成人免费4hu | 国产一区二区不卡在线 | 国产一区二区三区久久久久久久久 | 亚洲精品电影在线观看 | 91精品久久久久久久 | 伊人久操 | 久久66 | 久久久蜜桃一区二区人 | 91av久久 | 狠狠操夜夜操 | 成人午夜免费视频 | 国产麻豆乱码精品一区二区三区 | 在线国产区 | 欧美极品一区二区三区 | 女同久久另类99精品国产 | 欧美一区二区三区啪啪 | 国产精品美女久久久久aⅴ国产馆 | 成人在线一区二区 | 日韩在线 | 亚洲精品免费观看视频 | 日韩一区不卡 | 黄色一级免费大片 | 中文字幕一区二区三区四区不卡 |