
【題目】已知函數![]() .
.
(1)當![]() 時,求證:
時,求證:![]() ;
;
(2)討論函數![]() 的零點個數.
的零點個數.
【答案】(1)證明見解析;(2)見解析.
【解析】
(1)證法一:令![]() ,利用導數求出函數
,利用導數求出函數![]() 的最小值為
的最小值為![]() (其中
(其中![]() 為函數
為函數![]() 的極小值點),然后利用基本不等式即可得出證明;
的極小值點),然后利用基本不等式即可得出證明;
證法二:先證明![]() 成立,再證明出不等式
成立,再證明出不等式![]() ,利用不等式的基本性質可得出
,利用不等式的基本性質可得出![]() ;
;
(2)令![]() ,得出
,得出![]() ,等式兩邊取對數得
,等式兩邊取對數得![]() ,構造函數
,構造函數![]() ,分析函數
,分析函數![]() 的單調性,求出函數
的單調性,求出函數![]() 的最小值,對函數
的最小值,對函數![]() 最小值的符號進行分類討論,由此可得出函數
最小值的符號進行分類討論,由此可得出函數![]() 的零點個數.
的零點個數.
(1)證法一:令![]() ,
,![]() ,
,
![]() ,所以,函數
,所以,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,![]() ,
,![]() ,
,
![]() 存在
存在![]() ,使
,使![]() ,則
,則![]() ,可得
,可得![]() ,
,
由于函數![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 單調遞增.
單調遞增.
所以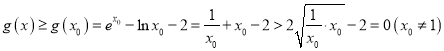 ,故原不等式成立;
,故原不等式成立;
證法二:先證明不等式![]() ,構造函數
,構造函數![]() ,其中
,其中![]() ,
,
則![]() 對任意的
對任意的![]() 恒成立,
恒成立,
所以,函數![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ,
,![]() .
.
同理可證![]() ,
,![]() ,則
,則![]() ,
,
即![]() ;
;
(2)令![]() ,得
,得![]() ,兩邊取對數得
,兩邊取對數得![]() ,
,
令![]() ,則
,則![]() ,令
,令![]() 得
得![]() .
.
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 單調遞增.
單調遞增.
![]() .
.
①當![]() 時,即
時,即![]() 得
得![]() 時,
時,![]() ,函數
,函數![]() 無零點;
無零點;
②當![]() 時,即
時,即![]() 得
得![]() 時,
時,![]() ,函數
,函數![]() 有
有![]() 個零點;
個零點;
③當![]() 時,即
時,即![]() 得
得![]() 時,
時,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
此時,函數![]() 在區間
在區間![]() 和區間
和區間![]() 上各有
上各有![]() 個零點.
個零點.
則函數![]() 有
有![]() 個零點.
個零點.
綜上所述,當![]() 時,函數
時,函數![]() 無零點;當
無零點;當![]() 時,函數
時,函數![]() 有
有![]() 個零點;當
個零點;當![]() 時,函數
時,函數![]() 有
有![]() 個零點.
個零點.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 與
與![]() 的公共點
的公共點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 且與
且與![]() 相切的直線交
相切的直線交![]() 于另一點
于另一點![]() ,過
,過![]() 且與
且與![]() 相切的直線交
相切的直線交![]() 于另一點
于另一點![]() ,記
,記![]() 為
為![]() 的面積.
的面積.
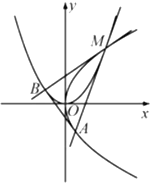
(Ⅰ)求![]() 的值(用
的值(用![]() 表示);
表示);
(Ⅱ)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
注:若直線與拋物線有且只有一個公共點,且與拋物線的對稱軸不平行也不重合,則稱該直線與拋物線相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北方的冬天戶外冰天雪地,若水管裸露在外,則管內的水就會結冰從而凍裂水管,給用戶生活帶來不便.每年冬天來臨前,工作人員就會給裸露在外的水管“保暖”:在水管外面包裹保溫帶,用一條保溫帶盤旋而上一次包裹到位.某工作人員采用四層包裹法(除水管兩端外包裹水管的保溫帶都是四層):如圖1所示是相鄰四層保溫帶的下邊緣輪廓線,相鄰兩條輪廓線的間距是帶寬的四分之一.設水管的直徑與保溫帶的寬度都為4cm.在圖2水管的側面展開圖中,此保溫帶的輪廓線與水管母線所成的角的余弦值是( )(保溫帶厚度忽略不計)
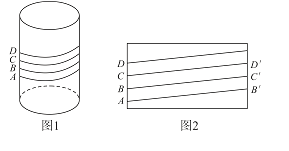
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三年級有男生![]() 人,學號為
人,學號為![]() ,
,![]() ,
,![]() ,
,![]() ;女生
;女生![]() 人,學號為
人,學號為![]() ,
,![]() ,
,![]() ,
,![]() .對高三學生進行問卷調查,按學號采用系統抽樣的方法,從這
.對高三學生進行問卷調查,按學號采用系統抽樣的方法,從這![]() 名學生中抽取
名學生中抽取![]() 人進行問卷調查(第一組采用簡單隨機抽樣,抽到的號碼為
人進行問卷調查(第一組采用簡單隨機抽樣,抽到的號碼為![]() );再從這
);再從這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人進行數據分析,則這
人進行數據分析,則這![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為內角
分別為內角![]() ,
,![]() ,
,![]() 的對邊,且滿
的對邊,且滿![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中,選出兩個使
這三個條件中,選出兩個使![]() 唯一確定的條件補充在下面的問題中,并解答問題.若________,________,求
唯一確定的條件補充在下面的問題中,并解答問題.若________,________,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】冠狀病毒是一個大型病毒家族,己知可引起感冒以及中東呼吸綜合征(![]() )和嚴重急性呼吸綜合征(
)和嚴重急性呼吸綜合征(![]() )等較嚴重疾病.而今年出現在湖北武漢的新型冠狀病毒(
)等較嚴重疾病.而今年出現在湖北武漢的新型冠狀病毒(![]() )是以前從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.
)是以前從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.
某醫院為篩查冠狀病毒,需要檢驗血液是否為陽性,現有n(![]() )份血液樣本,有以下兩種檢驗方式:
)份血液樣本,有以下兩種檢驗方式:
方式一:逐份檢驗,則需要檢驗n次.
方式二:混合檢驗,將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗.
)份血液樣本分別取樣混合在一起檢驗.
若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為![]() .
.
假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(![]() ).現取其中k(
).現取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]() .
.
(1)若![]() ,試求p關于k的函數關系式
,試求p關于k的函數關系式![]() ;
;
(2)若p與干擾素計量![]() 相關,其中
相關,其中![]() (
(![]() )是不同的正實數,
)是不同的正實數,
滿足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求證:數列![]() 等比數列;
等比數列;
(ii)當![]() 時,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數的期望值更少,求k的最大值
時,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數的期望值更少,求k的最大值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com