
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)設![]() ,證明:
,證明:![]() ,當
,當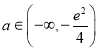 時,函數
時,函數![]() 恒有兩個不同零點.
恒有兩個不同零點.
【答案】(1)![]() 時,在
時,在![]() 上單調遞增;
上單調遞增;![]() 時,在
時,在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;(2)證明見解析
上單調遞減;(2)證明見解析
【解析】
(1)分別在![]() 和
和![]() 兩種情況下討論導函數的正負,從而得到原函數的單調性;
兩種情況下討論導函數的正負,從而得到原函數的單調性;
(2)將問題轉化為當 時,
時,![]() 與
與![]() 恒有兩個不同的交點的證明;利用導數可求得
恒有兩個不同的交點的證明;利用導數可求得![]() 的單調性和最值,從而確定
的單調性和最值,從而確定![]() 的范圍,解得
的范圍,解得![]() 的范圍.
的范圍.
(1)由題意得:![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增;
上單調遞增;
②當![]() 時,令
時,令![]() ,解得:
,解得:![]() ,
,
![]() 當
當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
綜上所述:當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)由題意得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,則問題等價于當
,則問題等價于當 時,
時,![]() 與
與![]() 恒有兩個不同的交點,
恒有兩個不同的交點,
![]() ,
,
![]() 當
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
![]() ,又
,又![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,
,
![]() 當
當![]() 時,
時,![]() 與
與![]() 恒有兩個不同的交點,
恒有兩個不同的交點,
即 ,
,![]() 與
與![]() 恒有兩個不同的交點,
恒有兩個不同的交點,
![]() 當
當 時,
時,![]() 在
在![]() 上恒有兩個不同的零點.
上恒有兩個不同的零點.


科目:高中數學 來源: 題型:
【題目】甲乙兩人同時參加一次數學測試,共有20道選擇題,每題均有4個選項,答對得3分,答錯或不答得0分,甲和乙都解答了所有的試題,經比較,他們只有2道題的選項不同,如果甲最終的得分為54分,那么乙的所有可能的得分值組成的集合為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() (
(![]() ,
,![]() )的部分圖象如圖中實線所示,圖中圓C與
)的部分圖象如圖中實線所示,圖中圓C與![]() 的圖象交于M,N兩點,且M在y軸上,則下列說法中正確的是( )
的圖象交于M,N兩點,且M在y軸上,則下列說法中正確的是( )

A.函數![]() 的最小正周期是2π
的最小正周期是2π
B.函數![]() 的圖象關于點
的圖象關于點![]() 成中心對稱
成中心對稱
C.函數![]() 在
在![]() 單調遞增
單調遞增
D.將函數![]() 的圖象向左平移
的圖象向左平移![]() 后得到的關于y軸對稱
后得到的關于y軸對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】極坐標系與直角坐標系xOy有相同的長度單位,以原點O為極點,以軸正半軸為極軸.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,射線
,射線![]() ,
,![]() ,
,![]() 與曲線
與曲線![]() 分別交于異于極點O的四點A,B,C,D.
分別交于異于極點O的四點A,B,C,D.
(1)若曲線![]() 關于
關于![]() 對稱,求
對稱,求![]() 的值,并求
的值,并求![]() 的參數方程;
的參數方程;
(2)若![]() |,當
|,當![]() 時,求
時,求![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用計算機生成隨機數表模擬預測未來三天降雨情況,規定1,2,3表示降雨,4,5,6,7,8,9表示不降雨,根據隨機生成的10組三位數:654 439 565 918 288 674 374 968 224 337,則預計未來三天僅有一天降雨的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】科赫曲線是一種外形像雪花的幾何曲線,一段科赫曲線可以通過下列操作步驟構造得到:任畫…條線段,然后把它分成三等分,以中間一段為邊向外作正三角形,并把中間一段去掉,這樣,原來的一條線段就變成了由4條小線段構成的折線,稱為“一次構造”;用同樣的方法把每一條小線段重復上述步驟,得到由16條更小的線段構成的折線,稱為“二次構造”;…;如此進行“n次構造”,就可以得到一條科赫曲線.若要在構造過程中使得到的折線的長度大于初始線段的100倍,則至少需要構造的次數是( )(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】滕州市公交公司一切為了市民著想,為方便市區學生的上下學,專門開通了學生公交專線,在學生上學、放學的時間段運行,為了更好地掌握發車間隔時間,公司工作人員對滕州二中車站發車間隔時間與侯車人數之間的關系進行了調查研究,現得到如下數據:
間隔時間 | 10 | 11 | 13 | 12 | 15 | 14 |
侯車人數 | 23 | 25 | 29 | 26 | 31 | 28 |
調查小組確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(1)求選取的2組數據不相鄰的概率;
(2)若選取的是前兩組數據,請根據后四組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的差均不超過1人,則稱為最佳回歸方程,在(2)中求出的回歸方程是否是最佳回歸方程?若規定一輛公交車的載客人數不超過35人,則間隔時間設置為18分鐘,是否合適?
參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() ,在
,在![]() 軸正半軸上有一點
軸正半軸上有一點![]() ,過點
,過點![]() 作直線
作直線![]() ,
,![]() 分別交拋物線于點
分別交拋物線于點![]() ,過點
,過點![]() 作
作![]() 垂直于
垂直于![]() 軸分別交
軸分別交![]() 于點
于點![]() .當
.當![]() ,直線
,直線![]() 的斜率為1時,
的斜率為1時,![]() .
.

(1)求拋物線的方程;
(2)判斷![]() 是否為定值,若是,求出此定值;若不是,請說明理由.
是否為定值,若是,求出此定值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com