
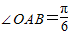 ��б߅AB=4��Rt��AOC����ͨ�^Rt��AOB��ֱ��AO���S���D(zhu��n)�õ����Ҷ����B-AO-C��ֱ����ǣ���(d��ng)�c(di��n)D��б߅AB�ϣ�
��б߅AB=4��Rt��AOC����ͨ�^Rt��AOB��ֱ��AO���S���D(zhu��n)�õ����Ҷ����B-AO-C��ֱ����ǣ���(d��ng)�c(di��n)D��б߅AB�ϣ�
 =
=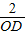 ����(d��ng)OD���r(sh��)��tan��CDO���
����(d��ng)OD��С�r(sh��)��tan��CDO���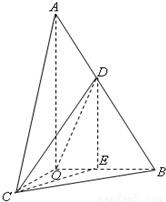 �⣺��I�����}�⣬CO��AO��BO��AO�����BOC�Ƕ����B-AO-C��ֱ����ǣ�
�⣺��I�����}�⣬CO��AO��BO��AO�����BOC�Ƕ����B-AO-C��ֱ����ǣ�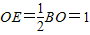 ��
��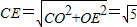 ��
��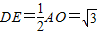 ��
��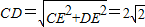
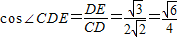 ��
��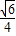 ����9�֣�
����9�֣�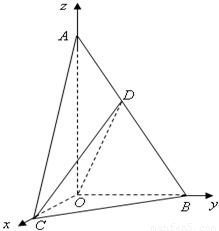 �ⷨ�����������gֱ������(bi��o)ϵO-xyz����D��
�ⷨ�����������gֱ������(bi��o)ϵO-xyz����D��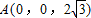 ��C��2��0��0����
��C��2��0��0����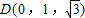 ��
��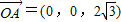 ��
��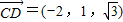 ��
��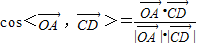 =
=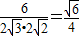 ��
��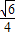 ����9�֣�
����9�֣�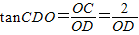 ����(d��ng)OD��С�r(sh��)����CDO����@�r(sh��)��OD��AB�������D��
����(d��ng)OD���r(sh��)����CDO����@�r(sh��)��OD��AB�������D��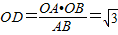 ��
��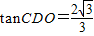 ��
��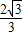 ����14�֣�
����14�֣�

 ���o(j��)��ͨ���w�n��С�W(xu��)�n�r(sh��)ͬ���_(d��)��(bi��o)ϵ�д�
���o(j��)��ͨ���w�n��С�W(xu��)�n�r(sh��)ͬ���_(d��)��(bi��o)ϵ�д� ���o(j��)��ͨ��(y��u)���y(c��)ϵ�д�
���o(j��)��ͨ��(y��u)���y(c��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
 ��D����Rt��AOB�У���OAB=
��D����Rt��AOB����OAB=| �� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
 ��D����Rt��AOB����OAB=
��D����Rt��AOB����OAB=| �� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
 ��D����Rt��AOB����OAB=
��D����Rt��AOB����OAB=| �� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
 ��D���� Rt��AOB�У���OAB=
��D���� Rt��AOB����OAB=| �� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
 ��2009•���Ӆ^(q��)һģ����D���� Rt��AOB�У���OAB=
��2009•���Ӆ^(q��)һģ����D���� Rt��AOB�У���OAB=| �� | 6 |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com