
經市場調查,某旅游城市在過去的一個月內(以30天計),旅游人數f(t)(萬人)與時間t(天)的函數關系近似滿足f(t)=4+ ,人均消費g(t)(元)與時間t(天)的函數關系近似滿足g(t)=115-|t-15|.
,人均消費g(t)(元)與時間t(天)的函數關系近似滿足g(t)=115-|t-15|.
(1)求該城市的旅游日收益w(t)(萬元)與時間t(1≤t≤30,t∈N*)的函數關系式;
(2)求該城市旅游日收益的最小值(萬元).
 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷3練習卷(解析版) 題型:選擇題
下列推理中屬于歸納推理且結論正確的是( )
A.設數列{an}的前n項和為Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推斷:Sn=n2
B.由f(x)=xcos x滿足f(-x)=-f(x)對?x∈R都成立,推斷:f(x)=xcos x為奇函數
C.由圓x2+y2=r2的面積S=πr2,推斷:橢圓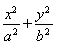 =1(a>b>0)的面積S=πab
=1(a>b>0)的面積S=πab
D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推斷:對一切n∈N*,(n+1)2>2n
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷1練習卷(解析版) 題型:選擇題
函數y=f(x),x∈D,若存在常數C,對任意的x1∈D,存在唯一的x2∈D使得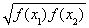 =C,則稱函數f(x)在D上的幾何平均數為C.已知f(x)=x3,x∈[1,2],則函數f(x)=x3在[1,2]上的幾何平均數為( )
=C,則稱函數f(x)在D上的幾何平均數為C.已知f(x)=x3,x∈[1,2],則函數f(x)=x3在[1,2]上的幾何平均數為( )
A. 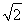 B.2
B.2
C.4 D.2 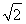
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練解答題押題練C組練習卷(解析版) 題型:解答題
某創業投資公司擬投資開發某種新能源產品,估計能獲得10萬元到1 000萬元的投資收益.現準備制定一個對科研課題組的獎勵方案:資金y(單位:萬元)隨投資收益x(單位:萬元)的增加而增加,且獎金不超過9萬元,同時獎金不超過投資收益的20%.
(1)若建立函數y=f(x)模型制定獎勵方案,試用數學語言表述該公司對獎勵函數f(x)模型的基本要求,并分析函數y=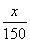 +2是否符合公司要求的獎勵函數模型,并說明原因;
+2是否符合公司要求的獎勵函數模型,并說明原因;
(2)若該公司采用模型函數y=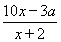 作為獎勵函數模型,試確定最小的正整數a的值.
作為獎勵函數模型,試確定最小的正整數a的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練解答題押題練B組練習卷(解析版) 題型:解答題
如圖,在四棱錐P ?ABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD為梯形,AB∥DC,AB⊥BC,PA=AB=BC,點E在棱PB上,且PE=2EB.
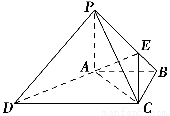
(1)求證:平面PAB⊥平面PCB;
(2)求證:PD∥平面EAC.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練填空題押題練F組練習卷(解析版) 題型:填空題
平面向量a,b滿足|a+2b|=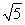 ,且a+2b平行于直線y=2x+1,若b=(2,-1),則a=________.
,且a+2b平行于直線y=2x+1,若b=(2,-1),則a=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練填空題押題練F組練習卷(解析版) 題型:填空題
若過正三角形ABC的頂點A任作一條直線l,則l與線段BC相交的概率為________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練填空題押題練B組練習卷(解析版) 題型:填空題
已知向量a=(3,1),b=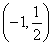 ,若a+λb與a垂直,則λ等于________.
,若a+λb與a垂直,則λ等于________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com