
【題目】已知函數f(x)= ![]() ,
,
(1)若m=2,求f(x)的最小值;
(2)若f(x)恰有2個零點,求實數m的取值范圍.
【答案】
(1)解:若m=2,則f(x)= ![]() ,
,
當1≤x<3時,f(x)=log3x﹣2,﹣2≤f(x)≤﹣1,f(x)min=﹣2
當x≥3時,f(x)=3(x﹣2)(x﹣4)=3(x﹣3)2﹣3,f(x)min=﹣3
∴f(x)的最小值為﹣3
(2)解:①若f(x)在1≤x<3時有1個零點,則m<0或 ![]() ,∴0≤m<1
,∴0≤m<1
此時需f(x)在x≥3時有1個零點,
∴ ![]() ∴m無解,
∴m無解,
②若f(x)在1≤x<3時無零點,則m<0或1﹣m≤0,即m<0或m≥1,此時f(x)在x≥3時有2個零點
當m<0時,f(x)在x≥3時無零點,不符合題意,
當m≥1時,f(x)在x≥3時有2個零點,則m≥3
綜上,m的取值范圍為[3,+![]() )
)
【解析】1、把m的值代入可得分段函數,分析每一個函數的最小值,分別根據對數函數的單調性可得當1≤x<3時,f(x)min=﹣2。當x≥3時,根據二次函數的最值情況求得f(x)min=﹣3,即最小值為-3.
2、利用反證法可得若f(x)在1≤x<3時有1個零點不成立,當m<0時,f(x)在x≥3時無零點,不符合題意故即得f(x)在x≥3時有2個零點成立則m≥3。


科目:高中數學 來源: 題型:
【題目】某媒體對“男女同齡退休”這一公眾關注的問題進行 了民意調査,右表是在某單位得到的數據(人數):
贊同 | 反對 | 合計 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合計 | 16 | 9 | 25 |
附表:
P(K2≥K) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
(1 )能否有90%以上的把握認為對這一問題的看法與性別有關?
【答案】解:解:K2= ![]() ≈2.932>2.706,
≈2.932>2.706,
由此可知,有90%的把握認為對這一問題的看法與性別有關
(1)進一步調查:(ⅰ)從贊同“男女同齡退休”16人中選出3人進行陳述發言,求事件“男士和女士各至少有1人發言”的概率; (ⅱ)從反對“男女同齡退休”的9人中選出3人進行座談,設參加調査的女士人數為X,求X的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在長方體ABCD﹣A1B1C1D1中,AA1=2AB=2BC,E,F,E1分別是棱AA1 , BB1 , A1B1的中點. 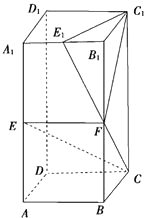
(1)求證:CE∥平面C1E1F;
(2)求證:平面C1E1F⊥平面CEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=sin (2x+ ![]() )的圖象可由函數y=cosx的圖象( )
)的圖象可由函數y=cosx的圖象( )
A.先把各點的橫坐標縮短到原來的 ![]() 倍,再向左平移
倍,再向左平移 ![]() 個單位
個單位
B.先把各點的橫坐標縮短到原來的 ![]() 倍,再向右平移
倍,再向右平移 ![]() 個單位
個單位
C.先把各點的橫坐標伸長到原來的2倍,再向左平移 ![]() 個單位
個單位
D.先把各點的橫坐標伸長到原來的2倍,再向右平移 ![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() (其中ω>0)
(其中ω>0)
(I)求函數f(x)的值域;
(II)若對任意的a∈R,函數y=f(x),x∈(a,a+π]的圖象與直線y=﹣1有且僅有兩個不同的交點,試確定ω的值(不必證明),并求函數y=f(x),x∈R的單調增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上函數f(x)是可導的,f(1)=2,且f(x)+f'(x)<1,則不等式f(x)﹣1<e1﹣x的解集是( )(注:e為自然對數的底數)
A.(1,+∞)
B.(﹣∞,0)∪(0,1)
C.(0,1)
D.(﹣∞,1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com