
(12分)(I)求函數(shù)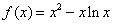 圖象上的點(diǎn)
圖象上的點(diǎn)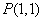 處的切線方程;
處的切線方程;
(Ⅱ)已知函數(shù)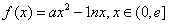 ,其中
,其中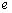 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),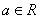
對于任意的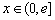 ,
,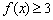 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)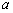 的取值范圍。
的取值范圍。
(1) (2)
(2)

【解析】
試題分析:解:(Ⅰ) ;
2分
;
2分
由題意可知切點(diǎn)的橫坐標(biāo)為1,
所以切線的斜率是 , 1分
, 1分
切點(diǎn)縱坐標(biāo)為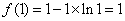 ,故切點(diǎn)的坐標(biāo)是
,故切點(diǎn)的坐標(biāo)是 ,
,
所以切線方程為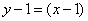 ,即
,即 .
2分
.
2分
(II)問題即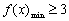 ,
,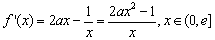 1分
1分
1)當(dāng)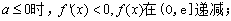
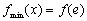
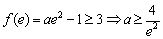 ,所以
,所以 無解。 (2分)
無解。 (2分)
2)當(dāng)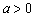 時(shí),
時(shí),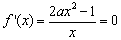 得
得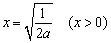
若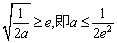 ,則
,則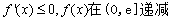 ,
,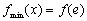
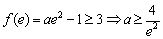 ,所以
,所以 無解。 (2分)
無解。 (2分)
若 時(shí),當(dāng)
時(shí),當(dāng) 時(shí)
時(shí)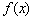 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng) 時(shí)
時(shí)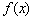 單調(diào)遞增。
單調(diào)遞增。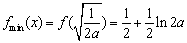 ,
,
綜上可知  (2分)
(2分)
考點(diǎn):導(dǎo)數(shù)的運(yùn)用
點(diǎn)評:根據(jù)導(dǎo)數(shù)求解函數(shù)的單調(diào)性,以及函數(shù) 極值和最值,屬于中檔題。


 陽光課堂課時(shí)作業(yè)系列答案
陽光課堂課時(shí)作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 (2012•廈門模擬)已知函數(shù)f(x)=Asin(2x+θ),其中A≠0,θ∈(0,
(2012•廈門模擬)已知函數(shù)f(x)=Asin(2x+θ),其中A≠0,θ∈(0,| π |
| 2 |
| π |
| 12 |
| π |
| 6 |
| 3 |
| ||
| 8 |
| PN |
| MN |
| ||
| 16 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆山東省日照市高三上學(xué)期第一次月考文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù)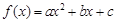 ,
,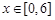 的圖象經(jīng)過
的圖象經(jīng)過 和
和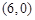 兩點(diǎn),如圖所示,且函數(shù)
兩點(diǎn),如圖所示,且函數(shù) 的值域?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2013121600363275459622/SYS201312160038234740271873_ST.files/image006.png">.過該函數(shù)圖象上的動(dòng)點(diǎn)
的值域?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2013121600363275459622/SYS201312160038234740271873_ST.files/image006.png">.過該函數(shù)圖象上的動(dòng)點(diǎn) 作
作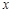 軸的垂線,垂足為
軸的垂線,垂足為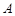 ,連接
,連接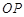 .
.
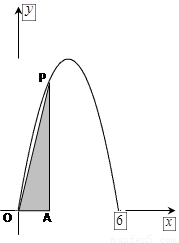
(I)求函數(shù) 的解析式;
的解析式;
(Ⅱ)記 的面積為
的面積為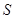 ,求
,求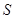 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年福建省高三第二次質(zhì)檢理科數(shù)學(xué)復(fù)習(xí)卷(二) 題型:解答題
.已知定義在R上的二次函數(shù) 滿足
滿足 ,且
,且 的最小值
的最小值
為0,函數(shù) ,又函數(shù)
,又函數(shù) 。
。
(I)求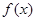 的單調(diào)區(qū)間; (II)當(dāng)
的單調(diào)區(qū)間; (II)當(dāng) ≤
≤ 時(shí),若
時(shí),若 ,求
,求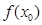 的最小值;
的最小值;
(III)若二次函數(shù) 圖象過(4,2)點(diǎn),對于給定的函數(shù)
圖象過(4,2)點(diǎn),對于給定的函數(shù)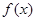 圖象上的點(diǎn)A(
圖象上的點(diǎn)A( ),
),
當(dāng) 時(shí),探求函數(shù)
時(shí),探求函數(shù)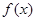 圖象上是否存在點(diǎn)
圖象上是否存在點(diǎn) (
( )(
)( ),使
),使 、
、 連線平行于
連線平行于 軸,并說明理由。(參考數(shù)據(jù):e=2.71828…)
軸,并說明理由。(參考數(shù)據(jù):e=2.71828…)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012屆山東省日照市高三上學(xué)期測評理科數(shù)學(xué)試卷 題型:解答題
已知定義在R上的二次函數(shù) 滿足
滿足 ,且
,且 的最小值為0,函數(shù)
的最小值為0,函數(shù) ,又函數(shù)
,又函數(shù)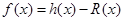 。
。
(I)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)當(dāng) ≤
≤ 時(shí),若
時(shí),若 ,求
,求 的最小值;
的最小值;
(III)若二次函數(shù) 圖象過(4,2)點(diǎn),對于給定的函數(shù)
圖象過(4,2)點(diǎn),對于給定的函數(shù) 圖象上的點(diǎn)A(
圖象上的點(diǎn)A( ),當(dāng)
),當(dāng) 時(shí),探求函數(shù)
時(shí),探求函數(shù) 圖象上是否存在點(diǎn)B(
圖象上是否存在點(diǎn)B( )(
)( ),使A、B連線平行于x軸,并說明理由。
),使A、B連線平行于x軸,并說明理由。
(參考數(shù)據(jù):e=2.71828…)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com