
【題目】已知函數![]() .
.
(Ⅰ)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)是否存在正整數![]() ,使得
,使得![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的最大值并給出推導過程,若不存在,說明理由.
的最大值并給出推導過程,若不存在,說明理由.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】試題分析:(I)求出![]() ,
, ![]() ,
, ![]() ,利用導數的幾何意義以及點斜式可得曲線
,利用導數的幾何意義以及點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(II)先根據
處的切線方程;(II)先根據![]() 時,可得
時,可得![]() ,所以若存在,則正整數
,所以若存在,則正整數![]() 的值只能取
的值只能取![]() ,
, ![]() ,
, ![]() 時,利用導數研究函數的單調性,可證明不等式恒成立,從而可得
時,利用導數研究函數的單調性,可證明不等式恒成立,從而可得![]() 的最大值
的最大值![]() .
.
試題解析:(Ⅰ)依題意![]()
則![]() ,
, ![]() ,
,
故所求切線方程為![]() .
.
(Ⅱ)依題意, ![]() ,故
,故![]() ,
,
故![]() 對一切
對一切![]() 恒成立,
恒成立,
當![]() 時,可得
時,可得![]() ,所以若存在,則正整數
,所以若存在,則正整數![]() 的值只能取
的值只能取![]() ,
, ![]() .
.
下面證明當![]() 時,不等式恒成立,
時,不等式恒成立,
設![]() ,則
,則![]() ,
,
易知![]() (
(![]() ),當
),當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
即![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數,
上是增函數,
所以![]() ,
,
當![]() 時,不等式恒成立,所以
時,不等式恒成立,所以![]() 的最大值是
的最大值是![]() .
.
【方法點晴】本題主要考查利用導數求曲線切線以及利用導數研究函數的單調性以及不等式恒成立問題,屬于難題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數,即
處的導數,即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數不存在,切線方程為
軸平行時,在 處導數不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


科目:高中數學 來源: 題型:
【題目】某人在靜水中游泳,速度為4![]() 公里/小時,他在水流速度為4公里/小時的河中游泳.
公里/小時,他在水流速度為4公里/小時的河中游泳.
(1)若他垂直游向河對岸,則他實際沿什么方向前進?實際前進的速度為多少?
(2)他必須朝哪個方向游,才能沿與水流垂直的方向前進?實際前進的速度為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=2px(p>0)的焦點為F,A為C上異于原點的任意一點,過點A的直線l交C于另一點B,交x軸的正半軸于點D,且有丨FA丨=丨FD丨.當點A的橫坐標為3時,△ADF為正三角形.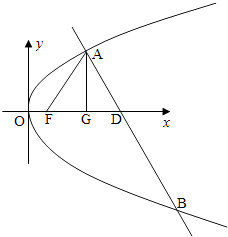
(1)求C的方程;
(2)若直線l1∥l,且l1和C有且只有一個公共點E,
(ⅰ)證明直線AE過定點,并求出定點坐標;
(ⅱ)△ABE的面積是否存在最小值?若存在,請求出最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某教師調查了![]() 名高三學生購買的數學課外輔導書的數量,將統計數據制成如下表格:
名高三學生購買的數學課外輔導書的數量,將統計數據制成如下表格:
男生 | 女生 | 總計 | |
購買數學課外輔導書超過 |
|
|
|
購買數學課外輔導書不超過 |
|
|
|
總計 |
|
|
|
(Ⅰ)根據表格中的數據,是否有![]() 的把握認為購買數學課外輔導書的數量與性別相關;
的把握認為購買數學課外輔導書的數量與性別相關;
(Ⅱ)從購買數學課外輔導書不超過![]() 本的學生中,按照性別分層抽樣抽取
本的學生中,按照性別分層抽樣抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人詢問購買原因,求恰有
人詢問購買原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,內角A,B,C所對的邊分別為a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com