
 (x∈R且x≠0)
(x∈R且x≠0) (x∈R且x≠0)
(x∈R且x≠0)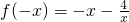 =-f(x)
=-f(x) 的單調遞減區間,
的單調遞減區間, 的單調遞增區間,
的單調遞增區間,
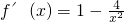
 的解析式,我們可以求出其導函數的解析式,進而根據導函數值大于0,函數為增函數,導函數值小于0,函數為減函數,得到當x>0時,函數f(x)的單調增區間和單調減區間.
的解析式,我們可以求出其導函數的解析式,進而根據導函數值大于0,函數為增函數,導函數值小于0,函數為減函數,得到當x>0時,函數f(x)的單調增區間和單調減區間.

科目:高中數學 來源:天利38套《2008全國各省市高考模擬試題匯編(大綱版)》、數學文 大綱版 題型:044
已知函數f(x)=x3+bx2+cx+d(b、c、d∈R且都為常數)的導函數為![]() ,且f(1)=7,設F(x)=f(x)-ax2(a∈R).
,且f(1)=7,設F(x)=f(x)-ax2(a∈R).
(Ⅰ)當a<2時,求F(x)的極小值;
(Ⅱ)若對任意的x∈[0,+∞),都有F(x)≥0成立,求a的取值范圍并證明不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源:新疆兵團二中2012屆高三第六次月考數學文科試題 題型:044
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<![]() )圖象如圖,P是圖象的最高點,Q為圖象與x軸的交點,O為原點.且|
)圖象如圖,P是圖象的最高點,Q為圖象與x軸的交點,O為原點.且|![]() |=2,|
|=2,|![]() |=
|=![]() ,|
,|![]() |=
|=![]() .
.

(Ⅰ)求函數y=f(x)的解析式;
(Ⅱ)將函數y=f(x)圖象向右平移1個單位后得到函數y=g(x)的圖象,當x∈[0,2]時,求函數h(x)=f(x)·g(x)的最大值.
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省南通市高三考前100題(二) (解析版) 題型:解答題
 (x>-2),求此函數的最小值.
(x>-2),求此函數的最小值. ,求y=4x-1+
,求y=4x-1+ 的最大值;
的最大值; 的最小值.
的最小值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com