
【題目】某省的一個氣象站觀測點在連續4天里記錄的AQI指數M與當天的空氣水平可見度y(單位:cm)的情況如下表:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
該省某市2019年12月份AQI指數M的頻數分布表如下:
M |
|
|
|
|
|
頻數 | 3 | 6 | 12 | 6 | 3 |
(1)設![]() ,若x與y之間具有線性關系,試根據上述數據求出y關于x的線性回歸方程;
,若x與y之間具有線性關系,試根據上述數據求出y關于x的線性回歸方程;
(2)王先生在該市開了一家洗車店,洗車店每天的平均收入與AQI指數的相關關系如下表:
M |
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
估計王先生的洗車店2019年12月份每天的平均收入.
附參考公式:![]() ,其中
,其中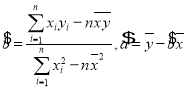
 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業者崗位分布條形圖,則下列結論中不一定正確的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.

A. 互聯網行業從業人員中90后占一半以上
B. 互聯網行業中從事技術崗位的人數超過總人數的20%
C. 互聯網行業中從事運營崗位的人數90后比80前多
D. 互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個有窮數列的每相鄰兩項之間插入這兩項的和,形成新的數列,我們把這樣的操作稱為該數列的一次“Z拓展”.如數列1,2第1次“Z拓展”后得到數列1,3,2,第2次“Z拓展”后得到數列1,4,3,5,2.設數列a,b,c經過第n次“Z拓展”后所得數列的項數記為Pn,所有項的和記為Sn.
(1)求P1,P2;
(2)若Pn≥2020,求n的最小值;
(3)是否存在實數a,b,c,使得數列{Sn}為等比數列?若存在,求a,b,c滿足的條件;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,過橢圓
中,過橢圓![]() :
:![]() 右焦點的直線
右焦點的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,且橢圓
兩點,且橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)![]() ,
,![]() 為
為![]() 上的兩點,若四邊形
上的兩點,若四邊形![]() 的對角線
的對角線![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過橢圓
,過橢圓![]() 的焦點且垂直于
的焦點且垂直于![]() 軸的直線被橢圓
軸的直線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 均在橢圓
均在橢圓![]() 上,點
上,點![]() 在拋物線
在拋物線![]() 上,若
上,若![]() 的重心為坐標原點
的重心為坐標原點![]() ,且
,且![]() 的面積為
的面積為![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如表:
元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如表:
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發生有責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機構為了研究某一品牌普通6座以下私家車的投保情況,隨機抽取了80輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
|
|
數量 | 20 | 10 | 10 | 20 | 15 | 5 |
以這80輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定,![]() .某同學家里有一輛該品牌車且車齡剛滿三年,記X為該品牌車在第四年續保時的費用,求X的分布列與數學期望值;(數學期望值保留到個位數字)
.某同學家里有一輛該品牌車且車齡剛滿三年,記X為該品牌車在第四年續保時的費用,求X的分布列與數學期望值;(數學期望值保留到個位數字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車.假設購進一輛事故車虧損4000元,一輛非事故車盈利8000元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司![]() 人數眾多
人數眾多![]() 為鼓勵員工利用網絡進行營銷,準備為員工辦理手機流量套餐.為了解員工手機流量使用情況,按照男員工和女員工
為鼓勵員工利用網絡進行營銷,準備為員工辦理手機流量套餐.為了解員工手機流量使用情況,按照男員工和女員工![]() 的比例分層抽樣,得到
的比例分層抽樣,得到![]() 名員工的月使用流量
名員工的月使用流量![]() (單位:
(單位:![]() )的數據,其頻率分布直方圖如圖所示.
)的數據,其頻率分布直方圖如圖所示.
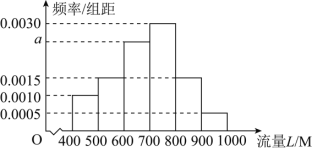
(1)求![]() 的值,并估計這
的值,并估計這![]() 名員工月使用流量的平均值
名員工月使用流量的平均值![]() (同一組中的數據用中點值代表
(同一組中的數據用中點值代表![]() ;
;
(2)若將月使用流量在![]() 以上(含
以上(含![]() )的員工稱為“手機營銷達人”,填寫下面的
)的員工稱為“手機營銷達人”,填寫下面的![]() 列聯表,能否有超過
列聯表,能否有超過![]() 的把握認為“成為手機營銷達人與員工的性別有關”;
的把握認為“成為手機營銷達人與員工的性別有關”;
男員工 | 女員工 | 合計 | |
手機營銷達人 | 5 | ||
非手機營銷達人 | |||
合計 | 200/span> |
參考公式及數據:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(3)若這![]() 名員工中有
名員工中有![]() 名男員工每月使用流量在
名男員工每月使用流量在![]() ,從每月使用流量在
,從每月使用流量在![]() 的員工中隨機抽取名
的員工中隨機抽取名![]() 進行問卷調查,記女員工的人數為
進行問卷調查,記女員工的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
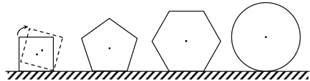
【題目】現有邊長均為1的正方形正五邊形正六邊形及半徑為1的圓各一個,在水平桌面上無滑動滾動一周,它們的中心的運動軌跡長分別為![]() ,
,![]() ,
,![]() ,
,![]() ,則( )
,則( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() .點
.點![]() 在橢圓
在橢圓![]() 上,點
上,點![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,直線
兩點,直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,且
,且![]() ,證明:
,證明:![]() 的面積是定值,并求此定值.
的面積是定值,并求此定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com