
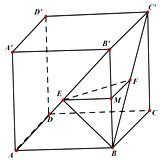
 如圖,在正方體ABCD-A'B'C'D'中,E,F分別是AB',BC'的中點.
如圖,在正方體ABCD-A'B'C'D'中,E,F分別是AB',BC'的中點.分析 (1)推導出ME∥AB,MF∥B′C′∥BC,由此能證明平面EMF∥平面ABCD.
(2)三棱錐M-EBF的體積VM-EBF=VB-MEF,由此能求出結果.
解答 證明:(1)∵在正方體ABCD-A'B'C'D'中,
E,F分別是AB',BC'的中點,M為BB'的中點,
∴ME∥AB,MF∥B′C′∥BC,
∵ME∩MF=M,AB∩BC=B,ME,MF?平面MEF,AB,BC?平面ABCD,
∴平面EMF∥平面ABCD.
解:(2)∵E,F分別是AB',BC'的中點,M為BB'的中點,
∴ME$\underset{∥}{=}$$\frac{1}{2}$AB=1,MF$\underset{∥}{=}$$\frac{1}{2}$BC=1,BM⊥平面MEF,BM=1,
∵AB⊥BC,∴EM⊥MF,
∴S△MEF=$\frac{1}{2}×ME×MF$=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
∴三棱錐M-EBF的體積:
VM-EBF=VB-MEF=$\frac{1}{3}×{S}_{△BEF}×BM$=$\frac{1}{3}×\frac{1}{2}×1=\frac{1}{6}$.
點評 本題考查面面平行的證明,考查三棱錐的體積的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x(公頃) | 20 | 40 | 50 | 60 | 80 |
| y(°C) | 3 | 4 | 4 | 4 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{3}-{y^2}=1$和 $\frac{y^2}{9}-\frac{x^2}{3}=1$ | B. | $\frac{x^2}{3}-{y^2}=1$和 ${y^2}-\frac{x^2}{3}=1$ | ||
| C. | ${y^2}-\frac{x^2}{3}=1$和 ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}-{y^2}=1$和$\frac{y^2}{3}-\frac{x^2}{9}=-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com