
已知 是正數(shù),
是正數(shù), ,
, ,
, .
.
(Ⅰ)若 成等差數(shù)列,比較
成等差數(shù)列,比較 與
與 的大小;
的大小;
(Ⅱ)若 ,則
,則 三個數(shù)中,哪個數(shù)最大,請說明理由;
三個數(shù)中,哪個數(shù)最大,請說明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整數(shù)部分分別是
的整數(shù)部分分別是

 求所有
求所有 的值.
的值.
(Ⅰ)
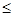
 ;(Ⅱ)
;(Ⅱ)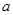 最大;(Ⅲ)
最大;(Ⅲ)
解析試題分析:(Ⅰ)用作差法比較大小,用對數(shù)的運算法則化簡后與0作比較。此時只需對數(shù)的真數(shù)與1作比較即可,根據(jù)單調(diào)性比得出對數(shù)和0的大小,從而得出 與
與 的大小。(Ⅱ)運用對數(shù)的運算法則將不等式化簡,再根據(jù)對數(shù)的單調(diào)性得真數(shù)的不等式,即關(guān)于a,b,c的不等式通過整理即可比較出三者中誰最大。(Ⅲ)由已知可得
的大小。(Ⅱ)運用對數(shù)的運算法則將不等式化簡,再根據(jù)對數(shù)的單調(diào)性得真數(shù)的不等式,即關(guān)于a,b,c的不等式通過整理即可比較出三者中誰最大。(Ⅲ)由已知可得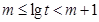 ,根據(jù)對數(shù)的運算法則可得
,根據(jù)對數(shù)的運算法則可得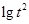 的范圍,得到其整數(shù)部分,根據(jù)已知其整數(shù)部分可列式求得
的范圍,得到其整數(shù)部分,根據(jù)已知其整數(shù)部分可列式求得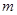 的可能取值。然后分情況討論,解對數(shù)不等式可求得
的可能取值。然后分情況討論,解對數(shù)不等式可求得 的值。
的值。
試題解析:解:(Ⅰ)由已知得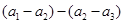 =
=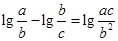 .
.
因為 成等差數(shù)列,所以
成等差數(shù)列,所以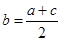 ,
,
則
 ,
,
因為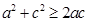 ,所以
,所以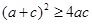 ,即
,即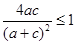 ,
,
則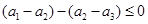 ,即
,即
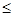
 ,當且僅當
,當且僅當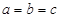 時等號成立.
時等號成立.
4分
(Ⅱ)解法1:令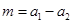 ,
,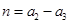 ,
,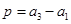 ,
,
依題意,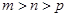 且
且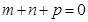 ,所以
,所以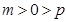 .
.
故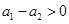 ,即
,即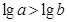 ;且
;且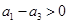 ,即
,即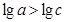 .
.
所以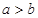 且
且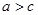 .
.
故 三個數(shù)中,
三個數(shù)中,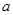 最大.
最大.
解法2:依題意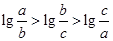 ,即
,即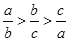 .
.
因為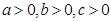 ,所以
,所以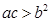 ,
,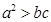 ,
,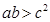 .
.
于是, ,
,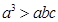 ,
,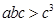 ,
,
所以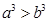 ,
,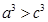 .
.
因為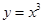 在
在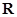 上為增函數(shù),所以
上為增函數(shù),所以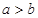 且
且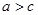 .
.
故 三個數(shù)中,
三個數(shù)中,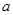 最大. 8分
最大. 8分
(Ⅲ)依題意, ,
,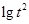 ,
,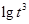 的整數(shù)部分分別是
的整數(shù)部分分別是

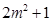 ,則
,則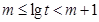 ,
,
所以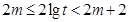 .
.
又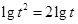 ,則
,則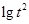 的整數(shù)部分是
的整數(shù)部分是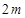 或
或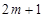 .
.
當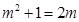 時,
時,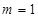 ;
;
當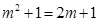 時,
時,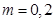 .
.
當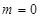 時,
時, ,
,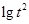 ,
,

科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=-x2+2ex+m-1,g(x)=x+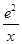 (x>0).
(x>0).
(1)若g(x)=m有零點,求m的取值范圍;
(2)確定m的取值范圍,使得g(x)-f(x)=0有兩個相異實根.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
為加快旅游業(yè)的發(fā)展,新余市2013年面向國內(nèi)發(fā)行總量為200萬張的“仙女湖之旅”優(yōu)惠卡,向省外人士發(fā)行的是金卡,向省內(nèi)人士發(fā)行的是銀卡.某旅游公司組織了一個有36名游客的旅游團到新余仙女湖旅游,其中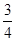 是省外游客,其余是省內(nèi)游客.在省外游客中有
是省外游客,其余是省內(nèi)游客.在省外游客中有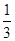 持金卡,在省內(nèi)游客中有
持金卡,在省內(nèi)游客中有 持銀卡.(1)在該團中隨機采訪2名游客,求恰有1人持銀卡的概率;
持銀卡.(1)在該團中隨機采訪2名游客,求恰有1人持銀卡的概率;
(2)在該團中隨機采訪2名游客,求其中持金卡與持銀卡人數(shù)相等概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某跨國飲料公司對全世界所有人均GDP(即人均純收入)在0.5—8千美元的地區(qū)銷售,該公司M飲料的銷售情況的調(diào)查中發(fā)現(xiàn):人均GDP處在中等的地區(qū)對該飲料的銷售量最多,然后向兩邊遞減.
(1)下列幾個模擬函數(shù)中(x表示人均GDP,單位:千美元;y表示年人均M飲料的銷量,單位:升),用哪個來描述人均,飲料銷量與地區(qū)的人均GDP的關(guān)系更合適?說明理由.
A.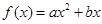 | B.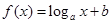 | C.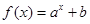 | D.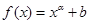 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
近日,國家經(jīng)貿(mào)委發(fā)出了關(guān)于深入開展增產(chǎn)節(jié)約運動,大力增產(chǎn)市場適銷對路產(chǎn)品的通知,并發(fā)布了當前國內(nèi)市場185種適銷工業(yè)品和42種滯銷產(chǎn)品的參考目錄。為此,一公司舉行某產(chǎn)品的促銷活動,經(jīng)測算該產(chǎn)品的銷售量P萬件(生產(chǎn)量與銷售量相等)與促銷費用x萬元滿足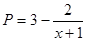 (其中
(其中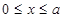 ,a為正常數(shù));已知生產(chǎn)該產(chǎn)品還需投入成本(10+2P)萬元(不含促銷費用),產(chǎn)品的銷售價格定為
,a為正常數(shù));已知生產(chǎn)該產(chǎn)品還需投入成本(10+2P)萬元(不含促銷費用),產(chǎn)品的銷售價格定為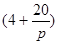 萬元/萬件.
萬元/萬件.
(1)將該產(chǎn)品的利潤y萬元表示為促銷費用x萬元的函數(shù);
(2)促銷費用投入多少萬元時,廠家的利潤是大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)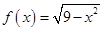 的定義域為集合
的定義域為集合 .
.
(1)若函數(shù) 的定義域也為集合
的定義域也為集合 ,
,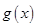 的值域為
的值域為 ,求
,求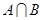 ;
;
(2)已知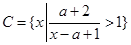 ,若
,若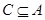 ,求實數(shù)
,求實數(shù)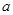 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)
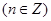 滿足
滿足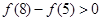 .
.
(1)求 的解析式;
的解析式;
(2)對于(1)中得到的函數(shù) ,試判斷是否存在
,試判斷是否存在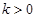 ,使
,使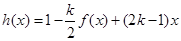 在區(qū)間
在區(qū)間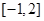 上的值域為
上的值域為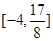 ?若存在,求出
?若存在,求出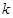 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知向量 ,
,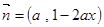 ,其中
,其中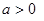 .函數(shù)
.函數(shù) 在區(qū)間
在區(qū)間 上有最大值為4,設
上有最大值為4,設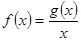 .
.
(1)求實數(shù)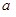 的值;
的值;
(2)若不等式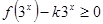 在
在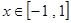 上恒成立,求實數(shù)
上恒成立,求實數(shù)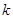 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)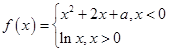 ,其中
,其中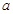 是實數(shù),設
是實數(shù),設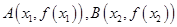 為該函數(shù)的圖象上的兩點,且
為該函數(shù)的圖象上的兩點,且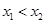 .
.
⑴指出函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
⑵若函數(shù) 的圖象在點
的圖象在點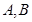 處的切線互相垂直,且
處的切線互相垂直,且 ,求
,求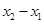 的最小值;
的最小值;
⑶若函數(shù) 的圖象在點
的圖象在點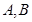 處的切線重合,求
處的切線重合,求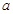 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com