

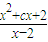 =a,且函數y=alnx+
=a,且函數y=alnx+ +c在(1,e)上具有單調性,則b的取值范圍是( )
+c在(1,e)上具有單調性,則b的取值范圍是( )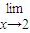
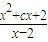 =a,求得a=1,c=-3,從而得到y=alnx+
=a,求得a=1,c=-3,從而得到y=alnx+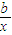 +c=
+c= ,再由“函數y=alnx+
,再由“函數y=alnx+ +c在(1,e)上具有單調性”轉化為“
+c在(1,e)上具有單調性”轉化為“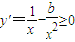 或
或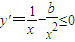 在(1,e)上恒成立”,再令t=
在(1,e)上恒成立”,再令t=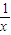 ∈(
∈(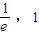 )轉化為-bt2+t≥0或-bt2+t≤0在(
)轉化為-bt2+t≥0或-bt2+t≤0在(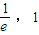 )上恒成立,由二次函數的性質求解.
)上恒成立,由二次函數的性質求解.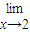
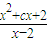 =a,
=a,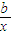 +c=
+c=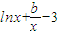
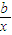 +c在(1,e)上具有單調性
+c在(1,e)上具有單調性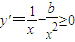 或
或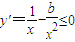 在(1,e)上恒成立
在(1,e)上恒成立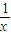 ∈(
∈(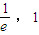 )
)

 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:高中數學 來源: 題型:單選題
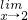
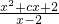 =a,且函數y=alnx+
=a,且函數y=alnx+ +c在(1,e)上具有單調性,則b的取值范圍是
+c在(1,e)上具有單調性,則b的取值范圍是查看答案和解析>>
科目:高中數學 來源:2010年江西省吉安市高考數學二模試卷(理科)(解析版) 題型:選擇題

 =a,且函數y=alnx+
=a,且函數y=alnx+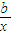 +c在(1,e)上具有單調性,則b的取值范圍是( )
+c在(1,e)上具有單調性,則b的取值范圍是( )查看答案和解析>>
科目:高中數學 來源:2010年天津市十二區縣重點學校高三聯考數學試卷1(理科)(解析版) 題型:選擇題
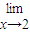
 =a,且函數y=alnx+
=a,且函數y=alnx+ +c在(1,e)上具有單調性,則b的取值范圍是( )
+c在(1,e)上具有單調性,則b的取值范圍是( )查看答案和解析>>
科目:高中數學 來源:2010年湖北省黃岡市名校高考數學模擬試卷07(理科)(解析版) 題型:選擇題
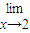
 =a,且函數y=alnx+
=a,且函數y=alnx+ +c在(1,e)上具有單調性,則b的取值范圍是( )
+c在(1,e)上具有單調性,則b的取值范圍是( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com