
(本小題滿分12分)為了了解某年段1000名學生的百米成績情況,隨機抽取了若干學生的百米成績,成績全部介于13秒與18秒之間,將成績按如下方式分成五組:第一組[13,14);第二組[14,15);……;第五組[17,18].按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前3個組的頻率之比為3∶8∶19,且第二組的頻數為8.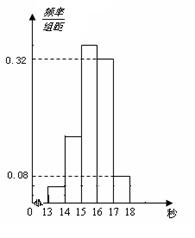
⑴將頻率當作概率,請估計該年段學生中百米成績在[16,17)內的人數;
⑵求調查中隨機抽取了多少個學生的百米成績;
⑶若從第一、五組中隨機取出兩個成績,求這兩個成績的差的絕對值大于1秒的概率.
(1)估計該年段學生中百米成績在[16,17)內的人數為320人。
(2)調查中隨機抽取了50個學生的百米成績. (3)P(A )= 。
。
解析試題分析:(1)根據頻率分步直方圖中小正方形的面積是這組數據的頻率,用長乘以寬得到面積,即為頻率.
(II)根據所有的頻率之和是1,列出關于x的方程,解出x的值做出樣本容量的值,即調查中隨機抽取了50個學生的百米成績.
(III)本題是一個古典概型,試驗發生所包含的事件是從第一、五組中隨機取出兩個成績,滿足條件的事件是成績的差的絕對值大于1秒,列舉出事件數,根據古典概型概率公式得到結果.
解:(1)百米成績在[16,17)內的頻率為0.32 1="0.32." 0.32
1="0.32." 0.32 1000=320
1000=320
∴估計該年段學生中百米成績在[16,17)內的人數為320人。 ……2分
(2)設圖中從左到右前3個組的頻率分別為3x,8x ,19x 依題意,得 3x+8x+19x+0.32 1+0.08
1+0.08 1="1" ,∴x=0.02 ……4分
1="1" ,∴x=0.02 ……4分
設調查中隨機抽取了n 個學生的百米成績,則 ∴n=50
∴n=50
∴調查中隨機抽取了50個學生的百米成績. ……6分
(3)百米成績在第一組的學生數有3 0.02
0.02 1
1 50=3,記他們的成績為a,b,c
50=3,記他們的成績為a,b,c
百米成績在第五組的學生數有0.08 1
1 50= 4,記他們的成績為m,n,p,q
50= 4,記他們的成績為m,n,p,q
則從第一、五組中隨機取出兩個成績包含的基本事件有
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},
{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21個 ……9分
設事件A為滿足成績的差的絕對值大于1秒,則事件A所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12個,……10分
所以P(A )= ……12分
……12分
考點:本試題主要考查了樣本估計總體,考查古典概型的概率公式,考查頻率分布直方圖等知識,考查數據處理能力和分析問題、解決問題的能力。
點評:解決該試題的關鍵是利用直方圖得到各個區間的概率值,進而結合古典概型概率公式,確定基本事件空間,和事件A發生的基本事件數,進而得到結論。


科目:高中數學 來源: 題型:解答題
2013年春節前,有超過20萬名廣西、四川等省籍的外來務工人員選擇駕乘摩托車沿321國道長途跋涉返鄉過年,為防止摩托車駕駛人因長途疲勞駕駛,手腳僵硬影響駕駛操作而引發交事故,肇慶市公安交警部門在321國道沿線設立了多個長途行駛摩托車駕乘人員休息站,讓過往返鄉過年的摩托車駕駛人有一個停車休息的場所。交警小李在某休息站連續5天對進站休息的駕駛人員每隔50輛摩托車就進行省籍詢問一次,詢問結果如圖所示:
(1)問交警小李對進站休息的駕駛人員的省籍詢問采用的是什么抽樣方法?
(2)用分層抽樣的方法對被詢問了省籍的駕駛人員進行抽樣,若廣西籍的有5名,則四川籍的應抽取幾名?
(3)在上述抽出的駕駛人員中任取2名,求抽取的2名駕駛人員中四川籍人數 的分布列及其數學期望。
的分布列及其數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分) 某班同學利用寒假在5個居民小區內選擇兩個小區逐戶進行一次“低碳生活習慣”的調查,以計算每戶的碳月排放量.若月排放量符合低碳標準的稱為“低碳族”,否則稱為“非低碳族”.若小區內有至少
某班同學利用寒假在5個居民小區內選擇兩個小區逐戶進行一次“低碳生活習慣”的調查,以計算每戶的碳月排放量.若月排放量符合低碳標準的稱為“低碳族”,否則稱為“非低碳族”.若小區內有至少 的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區” .若備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區” .若備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
(1)求所選的兩個小區恰有一個為“非低碳小區”的概率;
(2)假定選擇的“非低碳小區”為小區 ,調查顯示其“低碳族”的比例為1:2,數據如圖1所示,經過大力宣傳,三個月后又進行一次調查,數據如圖2所示,問這時小區
,調查顯示其“低碳族”的比例為1:2,數據如圖1所示,經過大力宣傳,三個月后又進行一次調查,數據如圖2所示,問這時小區 是否達到“低碳小區”的標準?
是否達到“低碳小區”的標準?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)某電視臺在一次對收看文藝節目和新聞節目觀眾的抽樣調查中,隨機抽取了100名電視觀眾,相關的數據如下表所示:
| | 文藝節目 | 新聞節目 | 總計 |
| 20至40歲 | 40 | 10 | 50 |
| 大于40歲 | 20 | 30 | 50 |
| 總計 | 60 | 40 | 100 |
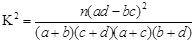
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題14分)下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量( 噸)與相應的生產能耗
噸)與相應的生產能耗 (噸)標準煤的幾組對照數據:
(噸)標準煤的幾組對照數據:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
 關于
關于 的線性回歸方程
的線性回歸方程 ;
; ,
, )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)為了調查甲、乙兩個交通站的車流量,隨機選取了14天,統計每天上午8∶00~12∶00間各自的車流量(單位:百輛),得如圖所示的統計圖,試求: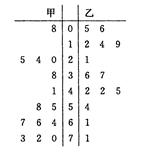
(1)甲、乙兩個交通站的車流量的極差分別是多少?
(2)甲交通站的車流量在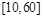 間的頻率是多少?
間的頻率是多少?
(3)根據該莖葉圖結合所學統計知識分析甲、乙兩個交通站哪個站更繁忙?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
某車間甲組有10名工人,其中有4名女工人;乙組有5名工人,其中有3名女工人,現在采用分層抽樣法(層內采用不放回的簡單隨機抽樣)從甲,乙兩組中共抽取3人進行技術考核.
(1)求甲,乙兩組各抽取的人數;
(2)求從甲組抽取的工人中恰有1名女工的概率;
(3)令X表示抽取的3名工人中男工人的人數,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為抗擊金融風暴,某系統決定對所屬企業給予低息貸款的扶持,該系統制定了評分標準,并根據標準對企業進行評估,然后依據評估得分將這些企業分別定為優秀、良好、合格、不合格四個等級,并根據等級分配相應的低息貸款數額,為了更好地掌握貸款總額,該系統隨機抽查了所屬的部分企業.一下圖表給出了有關數據(將頻率看做概率)
(1)任抽一家所屬企業,求抽到的企業等級是優秀或良好的概率;
(2)對照標準,企業進行了整改.整改后,如果優秀企業數量不變,不合格企業、合格企業、良好企業的數量成等差數列.要使所屬企業獲得貸款的平均值(即數學期望)不低于410萬元,那么整改后不合格企業占企業總數百分比的最大值是多少?

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
某種產品的廣告費支出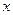 與銷售額
與銷售額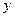 (單位:萬元)之間有如下對應數據:
(單位:萬元)之間有如下對應數據:
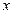 | 2 | 4 | 5 | 6 | 8 |
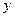 | 30 | 40 | 60 | 50 | 70 |
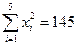
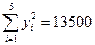
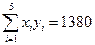 ,
,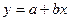 ,其中
,其中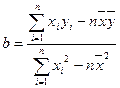 )
)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com