
【題目】某總公司在A,B兩地分別有甲、乙兩個下屬公司同種新能源產品(這兩個公司每天都固定生產50件產品),所生產的產品均在本地銷售.產品進人市場之前需要對產品進行性能檢測,得分低于80分的定為次品,需要返廠再加工;得分不低于80分的定為正品,可以進人市場.檢測員統計了甲、乙兩個下屬公司100天的生產情況及每件產品盈利虧損情況,數據如表所示:
表1
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件數 | 10 | 10 | 40 | 40 | 50 | |
天數 | 10 | 10 | 10 | 10 | 80 |
表2
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件數 | 10 | 5 | 40 | 45 | 50 | |
天數 | 20 | 10 | 20 | 10 | 70 |
表3
每件正品 | 每件次品 | |
甲公司 | 盈2萬元 | 虧3萬元 |
乙公司 | 盈3萬元 | 虧3.5萬元 |
(1)分別求甲、乙兩個公司這100天生產的產品的正品率(用百分數表示).
(2)試問甲、乙兩個公司這100天生產的產品的總利潤哪個更大?說明理由.
(3)若以甲公司這100天中每天產品利潤總和對應的頻率作為概率,從甲公司這100天隨機抽取1天,記這天產品利潤總和為X,求X的分布列及其數學期望.
【答案】(1)甲公司這100天生產的產品的正品率為:88%,乙公司這100天生產的產品的正率為:79%;(2)乙公司這100天生產的產品的總利潤更大;詳見解析;(3)分布列見詳解,數學期望為![]() 萬元.
萬元.
【解析】
(1)計算正品數與產品總數的比值即可;
(2)分別計算利潤,比較即可;
(3)計算X(單位:萬元)的可能取值為100,50,﹣150的概率,由期望的定義可得答案.
(1)甲公司這100天生產的產品的正品率為:![]() 88%,
88%,
乙公司這100天生產的產品的正率為:![]() 79%.
79%.
(2)乙公司這100天生產的產品的總利潤更大
理由如下:
甲公司這100天生產的產品的總利潤為(50×80+40×10)×2+(50×100﹣50×80﹣40×10)×(﹣3)=7000(萬元),
乙公司這100天生產的產品的總利潤為(50×70+45×10)×3+(50×100﹣50×70﹣45×10)×(﹣3.5)=8175(萬元),
因為7000萬<8175萬,所以乙公司這100天生產的產品的總利潤更大,
(3)X(單位:萬元)的可能取值為100,50,﹣150,
P(X=100)![]() 0.8.
0.8.
P(X=50)![]() 0.1,
0.1,
P(X=150)![]() 0.1,
0.1,
則X的分布列為
X | 100 | 50 | ﹣150 |
P | 0.8 | 0.1 | 0.1 |
故EX=100×0.8+50×0.1+(﹣150)×0.1=70(萬元),


科目:高中數學 來源: 題型:
【題目】某溫泉度假村擬以泉眼![]() 為圓心建造一個半徑為
為圓心建造一個半徑為![]() 米的圓形溫泉池,如圖所示,
米的圓形溫泉池,如圖所示,![]() 、
、![]() 是圓
是圓![]() 上關于直徑
上關于直徑![]() 對稱的兩點,以
對稱的兩點,以![]() 為圓心,
為圓心,![]() 為半徑的圓與圓
為半徑的圓與圓![]() 的弦
的弦![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() ,其中四邊形
,其中四邊形![]() 為溫泉區,I、II區域為池外休息區,III、IV區域為池內休息區,設
為溫泉區,I、II區域為池外休息區,III、IV區域為池內休息區,設![]() .
.
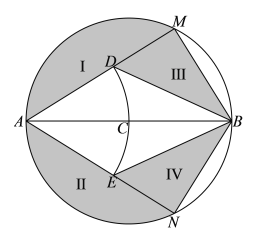
(1)當![]() 時,求池內休息區的總面積(III和IV兩個部分面積的和);
時,求池內休息區的總面積(III和IV兩個部分面積的和);
(2)當池內休息區的總面積最大時,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小芳、小明兩人各拿兩顆質地均勻的骰子做游戲,規則如下:若擲出的點數之和為4的倍數,則由原投擲人繼續投擲;若擲出的點數之和不是4的倍數,則由對方接著投擲.規定第一次從小明開始.
(1)求前4次投擲中小明恰好投擲2次的概率;
(2)設游戲的前4次中,小芳投擲的次數為![]() ,求隨機變量
,求隨機變量![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在發生某公共衛生事件期間,有專業機構認為該事件在一段時間內沒有發生大規模群體感染的標志是“連續10日,每天新增疑似病例不超過7人”.已知過去10日,![]() 、
、![]() 、
、![]() 三地新增疑似病例數據信息如下:
三地新增疑似病例數據信息如下:
![]() 地:總體平均數為3,中位數為4;
地:總體平均數為3,中位數為4;
![]() 地:總體平均數為2,總體方差為3;
地:總體平均數為2,總體方差為3;
![]() 地:總體平均數為1,總體方差大于0;
地:總體平均數為1,總體方差大于0;
則![]() 、
、![]() 、
、![]() 三地中,一定沒有發生大規模群體感染的是__________地.
三地中,一定沒有發生大規模群體感染的是__________地.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
B.命題“在△ABC中,若A>B,則sinA>sinB”的逆命題為假命題.
C.“![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
D.若“p或q”為真命題,則p,q至少有一個為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 上的一點,F為橢圓的右焦點,且
上的一點,F為橢圓的右焦點,且![]() 垂直于x軸,不過原點O的直線
垂直于x軸,不過原點O的直線![]() 交橢圓于A,B兩點,線段
交橢圓于A,B兩點,線段![]() 的中點M在直線
的中點M在直線![]() 上.
上.
(1)求橢圓C的標準方程;
(2)當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為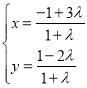 (
(![]() 為參數,且
為參數,且![]() ).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線
).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點P的極坐標為![]() ,Q為曲線
,Q為曲線![]() 上的動點,求
上的動點,求![]() 的中點M到曲線
的中點M到曲線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的非負半軸為極軸,建立極坐標系,并在兩種坐標系中取相同的長度單位.已知圓![]() 和圓
和圓![]() 的極坐標方程分別是
的極坐標方程分別是![]() 和
和![]() .
.
(1)求圓![]() 和圓
和圓![]() 的公共弦所在直線的直角坐標方程;
的公共弦所在直線的直角坐標方程;
(2)若射線![]() :
:![]() 與圓
與圓![]() 的交點為O、P,與圓
的交點為O、P,與圓![]() 的交點為O、Q,求
的交點為O、Q,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某飲料廠生產![]() 兩種飲料.生產1桶
兩種飲料.生產1桶![]() 飲料,需該特產原料100公斤,需時間3小時;生產1桶
飲料,需該特產原料100公斤,需時間3小時;生產1桶![]() 飲料需該特產原料100公斤,需時間1小時,每天
飲料需該特產原料100公斤,需時間1小時,每天![]() 飲料的產量不超過
飲料的產量不超過![]() 飲料產量的2倍,每天生產兩種飲料所需該特產原料的總量至多750公斤,每天生產
飲料產量的2倍,每天生產兩種飲料所需該特產原料的總量至多750公斤,每天生產![]() 飲料的時間不低于生產
飲料的時間不低于生產![]() 飲料的時間,每桶
飲料的時間,每桶![]() 飲料的利潤是每桶
飲料的利潤是每桶![]() 飲料利潤的1.5倍,若該飲料廠每天生產
飲料利潤的1.5倍,若該飲料廠每天生產![]() 飲料
飲料![]() 桶,
桶,![]() 飲料
飲料![]() 桶時(
桶時(![]() )利潤最大,則
)利潤最大,則![]() _____.
_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com