
【題目】如圖,三棱柱![]() 中,
中,![]() 分別為棱
分別為棱![]() 的中點.
的中點.
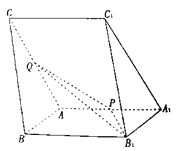
(1)在![]() 上確定點M,使
上確定點M,使![]() 平面
平面![]() ,并說明理由。
,并說明理由。
(2)若側面![]() 側面
側面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(1)答案見解析;(2)![]() .
.
【解析】
(1)取BC中點M,連接AM,則AM∥平面PQB1;利用面面平行證明線面平行即可;
(2)作QO⊥平面ABB1A1,與A1A延長線交于O,作PN∥C1A1,則直線A1C1與平面PQB1所成角即直線PN與平面PQB1所成角,結合幾何關系求解直線![]() 與平面
與平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
(1)取BC中點M,連接AM,則AM∥平面PQB1;
如圖所示,取BB1中點N,連結AM,AN,
![]() 為平行四邊形,點N,P為中點,則
為平行四邊形,點N,P為中點,則![]() ,由線面平行的判定定理可得
,由線面平行的判定定理可得![]() 平面PQB1,
平面PQB1,
同理可得,![]() 平面PQB1,
平面PQB1,
據此可得平面AMN∥平面PQB1,故![]() 平面
平面![]() .
.

(2)作QO⊥平面ABB1A1,與A1A延長線交于O,

則![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
作PN∥C1A1,則直線A1C1與平面PQB1所成角即直線PN與平面PQB1所成角,
![]() .
.
設N到平面PQB1的距離為h,則![]() ,
,
∴直線A1C1與平面PQB1所成角的正弦值為:![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 是
是![]() 上一點.
上一點.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是
是![]() 分別關于兩坐標軸及坐標原點的對稱點,平行于
分別關于兩坐標軸及坐標原點的對稱點,平行于![]() 的直線
的直線![]() 交
交![]() 于異于
于異于![]() 的兩點
的兩點![]() .點
.點![]() 關于原點的對稱點為
關于原點的對稱點為![]() .證明:直線
.證明:直線![]() 與
與![]() 軸圍成的三角形是等腰三角形.
軸圍成的三角形是等腰三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 、
、![]() 、
、![]() ,且
,且![]() 都有
都有![]() ,滿足
,滿足![]() 的實數
的實數![]() 有且只有
有且只有![]() 個,給出下述四個結論:
個,給出下述四個結論:
①滿足題目條件的實數![]() 有且只有
有且只有![]() 個;②滿足題目條件的實數
個;②滿足題目條件的實數![]() 有且只有
有且只有![]() 個;
個;
③![]() 在
在![]() 上單調遞增;④
上單調遞增;④![]() 的取值范圍是
的取值范圍是![]() .
.
其中所有正確結論的編號是( )
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市房產中心數據研究顯示,2018年該市新建住宅銷售均價如下表.3月至7月房價上漲過快,為抑制房價過快上漲,政府從8月份開始出臺了相關限購政策,10月份開始房價得到了很好的抑制.
均價(萬元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(Ⅰ)請建立3月至7月線性回歸模型(保留小數點后3位),并預測若政府不宏觀調控,12月份該市新建住宅銷售均價;
(Ⅱ)試用相關系數說明3月至7月各月均價![]() (萬元/
(萬元/![]() )與月份
)與月份![]() 之間可用線性回歸模型(保留小數點后2位)
之間可用線性回歸模型(保留小數點后2位)
參考數據:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
回歸方程斜率和截距最小二乘法估計公式 ;
;
相關系數 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年,新冠狀肺炎疫情牽動每一個中國人的心,危難時刻眾志成城,共克時艱,為疫區助力.福建省漳州市東山縣共101個海鮮商家及個人為緩解武漢物質壓力,募捐價值百萬的海鮮輸送武漢.東山島,別稱陵島,形似蝴蝶亦稱蝶島,隸屬于福建省漳州市東山縣,是福建省第二大島,中國第七大島,介于廈門市和廣東省汕頭之間,東南是著名的閩南漁場和粵東漁場交匯處,因地理位置發展海產品養殖業具有得天獨厚的優勢.根據養殖規模與以往的養殖經驗,某海鮮商家的海產品每只質量(克)在正常環境下服從正態分布![]() .
.
(1)隨機購買10只該商家的海產品,求至少買到一只質量小于265克該海產品的概率;
(2)2020年該商家考慮增加先進養殖技術投入,該商家欲預測先進養殖技術投入為49千元時的年收益增量.現用以往的先進養殖技術投入![]() (千元)與年收益增量
(千元)與年收益增量![]() (千元).
(千元).![]() 的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線
的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根據所給的統計量,求y關于x的回歸方程,并預測先進養殖技術投入為49千元時的年收益增量.
.根據所給的統計量,求y關于x的回歸方程,并預測先進養殖技術投入為49千元時的年收益增量.
附:若隨機變量![]() ,則
,則![]()
![]() ;
;
對于一組數據![]()
![]()
![]()
![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為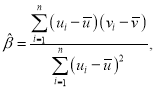
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com